Espacio de Hausdorff

Espacio de Hausdorff

Espacio de Hausdorff

En topología, un espacio de Hausdorff, separado o T2 es un espacio topológico en el que puntos distintos tienen entornos disjuntos.

Los espacios de Hausdorff se llaman así en honor de Felix Hausdorff, uno de los fundadores de la topología. La definición original de Hausdorff de un espacio topológico (de 1914) incluía la propiedad de Hausdorff como axioma.

Todo espacio métrico (y por lo tanto todo espacio normado) es un espacio de Hausdorff.

Definiciones

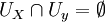Dados dos puntos x e y de un espacio topológico X, se dice que ambos puntos gozan de la propiedad de Hausdorff si existen dos entornos Ux de x y Uy de y tales que U_X \cap U_y = \empty.

Un espacio topológico se dice que es un espacio de Hausdorff, o que verifica la propiedad de Hausdorff, o que es T2, si todo par de puntos del espacio verifican la propiedad de Hausdorff.

Principales propiedades de los Espacios de Hausdorff.

Todo espacio de Hausdorff es también accesible o T_1, y por lo tanto también es un espacio T D y también un espacio de Kolmogórov o T0.

Así pues, por ser T1, todo conjunto unitario es cerrado.

Véase también

Obtenido de "Espacio de Hausdorff"

Wikimedia foundation. 2010.

Игры ⚽ Поможем сделать НИР

Mira otros diccionarios:

  • Espacio completamente de Hausdorff — Saltar a navegación, búsqueda En topología, espacios completamente de Hausdorff y espacios de Urysohn (o T2½) son tipos de espacios topológicos que satisfacen axiomas de separación más fuertes que los del espacio de Hausdorff. Contenido 1… …   Wikipedia Español

  • Espacio de Baire — Saltar a navegación, búsqueda En topología y ramas relacionadas de las matemáticas, un espacio de Baire es un espacio topológico que, hablando intuitivamente es muy grande y tiene suficientes puntos para un cierto proceso límite. Fue nombrado así …   Wikipedia Español

  • Espacio métrico — Saltar a navegación, búsqueda En matemática, un espacio métrico es un tipo particular de espacio topológico donde una distancia entre puntos está definida. Corresponde al caso muy común en que se dispone de una noción de distancia sobre el… …   Wikipedia Español

  • Espacio sobrio — Saltar a navegación, búsqueda En matemáticas, particularmente en topología, un espacio topológico X es sobrio si para todos los subconjuntos cerrados C de X que no contienen estrictamente un conjunto cerrado no vacío más pequeño, existe un único… …   Wikipedia Español

  • Espacio sobrio — En matemáticas, particularmente en topología, un espacio topológico X es sobrio si para todos los subconjuntos cerrados C de X que no contienen estrictamente un conjunto cerrado no vacío más pequeño, exi …   Enciclopedia Universal

  • Espacio paracompacto — Saltar a navegación, búsqueda En matemáticas, un espacio paracompacto es un espacio topológico en que todo recubrimiento por abiertos admite un refinamiento localmente finito. Por refinamiento de un recubrimiento de un espacio X se entiende un… …   Wikipedia Español

  • Espacio normal — Saltar a navegación, búsqueda En Topología y ramas relacionadas de la matemática, los espacios normales, espacios T4, y espacios T5 son tipos particulares de espacios topológicos. Estas condiciones son ejemplos de Axiomas de separación.… …   Wikipedia Español

  • Espacio (desambiguación) — Saltar a navegación, búsqueda Espacio es un concepto abstracto utilizado en matemática, física, filosofía, informática, y otras ciencias. El término espacio, también puede referirse a: En astronomía y exploración espacial: Espacio exterior,… …   Wikipedia Español

  • Espacio uniforme — Saltar a navegación, búsqueda En topología, espacios uniformes son aquellos utilizados para estudiar conceptos como la continuidad uniforme, completitud y convergencia uniforme. Los espacios uniformes generalizan los espacios métricos y abarcan… …   Wikipedia Español

  • Hausdorff — En matemáticas Hausdorff puede referirse a diferentes conceptos: Al matemático Felix Hausdorff. En topología, un espacio Hausdorff, es aquel que satisface el axioma T2 de separación. En análisis matemático, a la distancia de Hausdorff entre dos… …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”