Número imaginario

Número imaginario
Ilustración del plano complejo. Los números imaginarios se encuentran en el eje de coordenadas vertical.

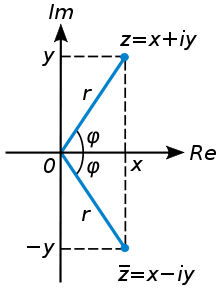
Un número imaginario es un número cuyo cuadrado es negativo(\sqrt{-1}\cdot\sqrt{-1}=-1). Fue en el año 1777 cuando Leonhard Euler le dio a \sqrt{-1} el nombre de i, por imaginario de manera despectiva dando a entender que no tenían una existencia real. Aunque si suponemos un plano con ejes cartesianos en el que los reales se encuentran sobre el eje horizontal y los imaginarios sobre el eje vertical, complejo, estos son un concepto totalmente válido. Gottfried Leibniz, en el siglo XVII, decía que \sqrt{-1} era una especie de anfibio entre el ser y la nada.

En campos de ingeniería eléctrica, electrónica y relacionados, la unidad imaginaria es a menudo escrita como j para evitar la confusión con la intensidad de una corriente eléctrica, tradicionalmente denotada por i.



Propiedades

\ldots (se repite el patrón
de la zona azul)
i^{-3} = i\,
i^{-2} = -1\,
i^{-1} = -i\,
i^0 = 1\,
i^1 = i\,
i^2 = -1\,
i^3 = -i\,
i^4 = 1\,
i^5 = i\,
i^6 = -1\,
\ldots (se repite el patrón
de la zona azul)

Todo número imaginario puede ser escrito como ib donde b es un número real e i es la unidad imaginaria, con la propiedad

i^2 = -1\,\!,

puesto entonces:

(bi)^2 = -b^2 \;

que es un número real.

Cada número complejo puede ser escrito unívocamente como una suma de un número real y un número imaginario, de esta forma:

a + bi \,\!

Al número imaginario i se le denomina también constante imaginaria.

Del mismo modo, partiendo de:

\sqrt{-1} = i

la raíz cuadrada de cualquier número real negativo, da por resulta un número imaginario, así por ejemplo:

\sqrt{-36} = \sqrt{(36)(-1)} = \sqrt{36} \, \sqrt{-1} = 6\; i

Estos números extienden el conjunto de los números reales \R al conjunto de los números complejos \mathbb{C}.

Usos

  • La unidad imaginaria puede ser usada para extender formalmente la raíz cuadrada de números negativos, confirmando el teorema fundamental del algebra.
  • Igualmente la raíz cuadrada de un número imaginario es un número complejo, y la raíz de un número complejo en general es otro número complejo.
  • Gracias a la fórmula de De Moivre los logaritmos de números negativos también son expresables (de manera no unívoca) mediante \ i, así \ ln(-1) = \pi i aunque cualquier número imaginario de la forma \ x = 2(n+1)\pi i satisface que \ e^x = -1. Curiosamente, i^i = e^{\log {i^i}} = e^{i \log{i}} = e^{- {\pi \over2}} \approx 0,2078795764.
  • En física cuántica la unidad imaginaria permite simplificar la descripción matemática de los estados cuánticos variables en el tiempo.
  • En teoría de circuitos y corriente alterna la unidad imaginaria se usa para representar ciertas magnitudes como fasores, lo cual permite un tratamiento algebraico más ágil de dichas magnitudes.

Véase también

Números
Complejos \mathbb{C}
Reales \mathbb{R}
Racionales \mathbb{Q}
Enteros \mathbb{Z}
Naturales \mathbb{N}
Uno
Primos
Compuestos
Cero
Negativos
Fraccionarios
Fracción propia
Fracción impropia
Irracionales
Algebraicos irracionales
Trascendentes
Imaginarios


Wikimedia foundation. 2010.

Игры ⚽ Поможем решить контрольную работу

Mira otros diccionarios:

  • Número imaginario — ► locución MATEMÁTICAS Raíz cuadrada de un número negativo cuya representación es la letra i. * * * Un número imaginario es un número cuyo cuadrado es negativo. El término fue acuñado por René Descartes en el decimoséptimo siglo y se propuso para …   Enciclopedia Universal

  • número — (Del lat. numĕrus). 1. m. Mat. Expresión de una cantidad con relación a su unidad. 2. Signo o conjunto de signos con que se representa el número. 3. Cantidad de personas o cosas de determinada especie. 4. Condición, categoría, situación o clase… …   Diccionario de la lengua española

  • imaginario — imaginario, ria (Del lat. imaginarĭus). 1. adj. Que solo existe en la imaginación. 2. Se decía del estatuario o del pintor de imágenes. 3. f. Mil. Suplente de un servicio. 4. Mil. Vigilancia que se hace por turno durante la noche en cada… …   Diccionario de la lengua española

  • Número (desambiguación) — Número puede en distintas disciplinas puede referise a diferentes conceptos: Contenido 1 Número como forma gramatical 2 Número como cantidad 3 Números usados para identificación 4 …   Wikipedia Español

  • Número — (Del lat. numerus.) ► sustantivo masculino 1 MATEMÁTICAS Ente abstracto o expresión de la cantidad en relación con la unidad. 2 MATEMÁTICAS Signo o conjunto de signos con que se representa este ente abstracto. SINÓNIMO cifra guarismo 3 Cantidad… …   Enciclopedia Universal

  • imaginario — (Del lat. imaginarius.) ► adjetivo 1 Que existe en la imaginación o fantasía y no en la realidad: ■ el eje de la Tierra es una línea imaginaria. SINÓNIMO fantástico ficticio figurado ideal prodigioso ► adjetivo/ sustantivo …   Enciclopedia Universal

  • Número complejo — Ilustración del plano complejo. Los números reales se encuentran en el eje de coordenadas horizontal y los imaginarios en el eje vertical. El término número complejo describe la suma de un número real y un número imaginario (que es un múltiplo… …   Wikipedia Español

  • Número complejo — ► locución MATEMÁTICAS El formado por la suma algebraica de un número real con uno imaginario. * * * Definición Los Números Complejos son una extensión de los números reales, cumpliéndose que . Los números complejos tienen la capacidad de… …   Enciclopedia Universal

  • número — {{＃}}{{LM N27648}}{{〓}} {{SynN28320}} {{［}}número{{］}} ‹nú·me·ro› {{《}}▍ s.m.{{》}} {{＜}}1{{＞}} Concepto matemático que expresa una cantidad con relación a una unidad: • En esta cuenta has sumado mal dos números.{{○}} {{＜}}2{{＞}} Signo o conjunto… …   Diccionario de uso del español actual con sinónimos y antónimos

  • Número real — Los números reales se definen de manera intuitiva como el conjunto de números que se encuentran en relación biyectiva con los puntos de una recta infinita: la recta numérica. El conjunto de los números reales se expresa por la letra . El nombre… …   Enciclopedia Universal

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”