Cuantificador universal

Cuantificador universal

En lógica matemática, se usa el símbolo \forall , denominado cuantificador universal, antepuesto a una variable para decir que "para todo" elemento de un cierto conjunto se cumple la proposición dada a continuación. En texto se puede representar con el carácter ∀.

Normalmente, en lógica, el conjunto al que se refiere es el universo o dominio de referencia, en el cual aparecen todas las constantes.

Ejemplo

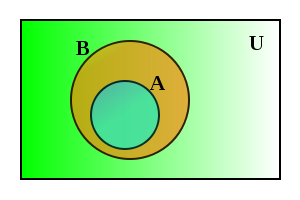
Conjuntos 04.svg

Si tenemos dos conjuntos diferentes A y B, y A es un subconjunto de B:

A \subset B \; \land \; A \not= B

Todo elemento x de A pertenece a B:

\forall x \in A \; \Rightarrow \; x \in B \,

Al ser A y B conjuntos diferentes como indica el diagrama, podemos decir que no todos los elementos y de B pertenecen a A, siendo esto una garantia suficiente para que dos conjuntos cualesquiera puedan ser diferentes:

\lnot \forall y \in B \; \Rightarrow \; y \in A \,

Es decir, que no para todo elemento y de B tenemos que o implica que y también pertenezca a A.

Relación cuantificador universal y el cuantificador existencial

Dada una expresión P(x), según el cuantificador universal se puede transformar en otra equivalente con el cuantificador existencial:

\forall x \ P(x) \; \Leftrightarrow \; \lnot \exists x \ \lnot P(x) \,

que podriamos leer: si para todo x se cumple P(x) no existe un x que no cumpla P(x).

Según el ejemplo anterior:

\forall x \in A \; \Rightarrow \; x \in B \,

Para todo x que pertenece a A implica que x pertenece a B, que podemos expresar:

\lnot \exists x \in B \; \Rightarrow \; x \notin A \,

No existe un x de B por tanto x no este en a A.

Véase también


Wikimedia foundation. 2010.

Игры ⚽ Нужен реферат?

Mira otros diccionarios:

  • Cuantificador universal — En lógica y matemáticas, se usa el símbolo ∀, denominado cuantificador universal, antepuesto a una variable para decir que «para todo» elemento de un cierto conjunto se cumple la proposición dada a continuación. Normalmente, en lógica, el… …   Enciclopedia Universal

  • Cuantificador — Saltar a navegación, búsqueda En Teoría de conjuntos, un cuantificador se utiliza para indicar cuántos elementos de un conjunto dado cumplen con cierta propiedad. Existen tres tipos de cuantificadores, cuyas características resumimos en la… …   Wikipedia Español

  • cuantificador — 1. m. Elemento o palabra que cuantifica. 2. Mat. Símbolo antepuesto que relaciona una o más variables con una cantidad. cuantificador existencial. m. Mat. Símbolo que indica que existe al menos un elemento de un conjunto que cumple una… …   Diccionario de la lengua española

  • Universal — puede referirse a: Universal (filosofía) Universal (metafísica) Conjunto universal Proposición universal Cuantificador universal Universal Music Group Universal Studios Universal Edition El Universal, nombre de diversos diarios en América Latina …   Wikipedia Español

  • universal — (Del lat. universālis, y este formado sobre el gr. καθολικός). 1. adj. Perteneciente o relativo al universo. 2. Que comprende o es común a todos en su especie, sin excepción de ninguno. 3. Que lo comprende todo en la especie de que se habla. 4.… …   Diccionario de la lengua española

  • cuantificador — ► sustantivo masculino 1 LÓGICA Elemento que se usa para expresar la cantidad en un enunciado o un juicio. 2 LINGÜÍSTICA Determinante que expresa idea de cantidad: ■ todo y dos son cuantificadores. * * * cuantificador. m. Elemento o palabra que… …   Enciclopedia Universal

  • Cuantificador existencial — En el lenguaje de predicados en lógica matemática, se usa el símbolo: , llamado cuantificador existencial, antepuesto a una variable para decir que existe al menos un elemento del conjunto al que hace referencia la variable, que cumple la… …   Wikipedia Español

  • universal — (Del lat. universalis.) ► adjetivo 1 ASTRONOMÍA Del universo o espacio celeste: ■ ley de gravitación universal. 2 Que pertenece o se extiende a todo el mundo: ■ el amor es un sentimiento universal. ANTÓNIMO individual 3 Que es común a un grupo de …   Enciclopedia Universal

  • Lógica de primer orden — La lógica de primer orden, también llamada lógica de predicados o cálculo de predicados, es un sistema formal diseñado para estudiar la inferencia en los lenguajes de primer orden.[1] Los lenguajes de primer orden son, a su vez, lenguajes… …   Wikipedia Español

  • Forma normal de Skolem — Este artículo o sección necesita referencias que aparezcan en una publicación acreditada, como revistas especializadas, monografías, prensa diaria o páginas de Internet fidedignas. Puedes añadirlas así o avisar …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”