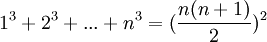En aritmética y álgebra, el cubo de un número n es la tercera potencia —el resultado de multiplicar por sí mismo dos veces:^[1]

n ³ = n × n × n

En geometría, es la ecuación para obtener el volumen de un cubo de lado n.

Contenido 1 Historia 2 Definiciones 3 Secuencia de cubos 4 Propiedades 5 Relación con otras funciones 6 Referencias 7 Enlaces externos

Historia

La determinación del cubo de grandes números ha sido una preocupación desde las civilizaciones muy antiguas. El antiguo matemático indio Aryabhatta en su obra matemática Aryabhatiya ya explica acerca del significado matemático del cubo (Aryabhatiya,(2-3), como "El producto de tres iguales al igual que el sólido que tiene 12 lados iguales, se denomina "cubo". Definiciones similares pueden verse en textos antiguos tales como el Brahmasphuta Siddhanta (XVIII. 42), Ganitha sara sangraha (II. 43) y el Siddhanta sekhara (XIII. 4). Es interesante observar que en la matemática moderna el término "cubo" tiene dos significados matemáticos al igual que en Sánscrito, donde la palabra Ghhana significa un factor de una potencia con el número, multiplicado a sí mismo tres veces en una estructura cúbica.

Definiciones

Un cubo perfecto (también llamado número cúbico, o a veces simplemente cubo) es un número que es el cubo de un número entero.

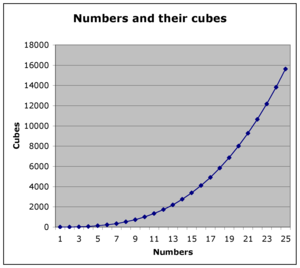
Secuencia de cubos

La secuencia de los números no-negativos de los cubos perfectos comienza como: A000578:

0, 1, 8, 27, 64, 125, 216, 343, 512, 729, 1000, 1331, 1728, 2197, 2744, 3375, 4096, 4913, 5832, 6859, 8000, 9261, 10648,

12167, 13824, 15625, 17576, 19683, 21952, 24389, 27000, 29791, 32768, 35937, 39304, 42875, 46656, 50653, 54872, 59319, 64000,

68921, 74088, 79507, 85184, 91125, 97736, 103823, 110592, 117649, 125000, 132651, 140608, 148877, 157464, 166375, 175616,

185193, 195112, 205379, 216000, 226981, 238328...

Propiedades

A diferencia del cuadrado de un número, no existe el número cubo más pequeño, debido a que se incluyen los números negativos. Por ejemplo, (−4) × (−4) × (−4) = −64. Para cualquier n, (−n)³ = −(n³).

A diferencia de los cuadrados perfectos, los cubos perfectos no tienen una pequeña cantidad de posibilidades excepto para los dos últimos dígitos. Excepto para los cubos divisibles por 5, donde únicamente 25 y 75 pueden ser los dos últimos dígitos, cualquier par de dígitos con los últimos dígitos impares puede ser un cubo perfecto. Con los cubos pares, hay una considerable restricción, solo para 00, i2, i4, p6 y i8 puede que los dos últimos dígitos de un cubo perfecto (donde o significa cualquier dígito impar y p para dígitos pares). Algunos números cúbicos son también números cuadrados, por ejemplo 64 es un cuadrado (8 × 8) y al mismo tiempo un cubo (4 × 4 × 4); esto ocurre si y solo si es una sexta potencia perfecta.

Esto es, sin embargo fácil de ver que la mayoría de los números no son cubos perfectos a causa de que todos los perfectos cubos deben tener una raíz digital 1, 8 o 9. De esta forma, la raíz digital de cualquier número puede dar determinada por el resto del número cuando es dividido entre 3:

• Si el número es divisible entre 3, su cubo tiene como raíz digital al 9;
• Si tiene como resto de 1 cuando es dividido entre 3, su cubo tiene la raíz digital igual a 1;
• Si tiene como resto de 2 cuando es dividido entre 3, su cubo tiene como raíz digital 8.

Cada entero positivo puede ser escrito como la suma de nueve cubos o incluso menos, véase problema de Waring. Este límite superior de nueve cubos no puede ser reducido ya que, por ejemplo, 23 no puede ser escrito como la suma de menos nueve cubos:

23 = 2³ + 2³ + 1³ + 1³ + 1³ + 1³ + 1³ + 1³ + 1³

El número m es un perfecto cubo si y solo si puede ordenarse m puntos en un cubo, por ejemplo 3 × 3 × 3 = 27. La suma de los primeros n cubos perfectos es un n-ésimo número triangular al cuadrado:

Por ejemplo, la suma de los primeros cinco números cubos perfectos, 1³ + 2³ + 3³ + 4³ + 5³, es igual a la suma de los cinco primeros números triangulares 15² que es 225.

Relación con otras funciones

La función inversa a encontrar un número cuyo cubo es n se denomina extracción de la raíz cúbica de n. La operación es similar a encontrar el lado de un cubo de volumen conocido. También se dice que n elevado un tercio.

Referencias

Enlaces externos

• Una Applet JAVA que descompone un número entero en otro no congruente 4 o 5 (mod 9) en suma de cuatro cubos.