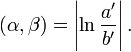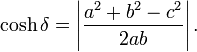La distancia inversiva se define así: Si dos círculos (α y β) que no se crucen se invierten en un círculo situado en un punto límite del pencil de α y β, entonces los inversos de α y β son concéntricos. Si a' y b' son los radios de los círculos concéntricos, entonces la distancia inversiva es

Además, si a y b son los radios de α y β (a diferencia de sus inversos), y c es la distancia entre sus centros, entonces la distancia inversiva δ es igual a

Referencias

• Coxeter, H. S. M.; S. L. Greitzer (1967). Geometry Revisited (en inglés). Washington: MAA. ISBN 0883856190.