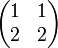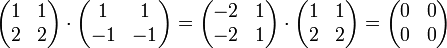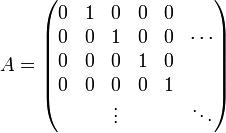Divisor de cero

Divisor de cero

Divisor de cero

En álgebra abstracta, un elemento no nulo a de un anillo A es un divisor de cero por la izquierda si existe un elemento no nulo b tal que ab = 0. Los divisores de cero por la derecha se definen análogamente. Un elemento que es tanto un divisor de cero por la izquierda como por la derecha recibe el nombre de divisor de cero. Si el producto es conmutativo, entonces no hace falta distinguir entre divisores de cero por la izquierda y por la derecha. Un elemento no nulo que no sea un divisor de cero ni por la izquierda ni por la derecha recibe el nombre de regular.

Ejemplos

El anillo Z de los enteros no tiene divisores de cero, pero en el anillo Z² (donde la suma y el producto se realizan componente a componente), se tiene que (0,1) × (1,0) = (0,0), así que tanto (0,1) como (1,0) son divisores de cero.

En el anillo cociente Z/6Z, la clase del 4 es un divisor de cero, ya que 3×4 es congruente con 0 módulo 6.

Un ejemplo de divisor de cero en el anillo de matrices de 2×2 es la siguiente matriz:

\begin{pmatrix}1&1\\ 2&2\end{pmatrix}

porque, por ejemplo,

\begin{pmatrix}1&1\\ 2&2\end{pmatrix}\cdot\begin{pmatrix}1&1\\ -1&-1\end{pmatrix}=\begin{pmatrix}-2&1\\ -2&1\end{pmatrix}\cdot\begin{pmatrix}1&1\\ 2&2\end{pmatrix}=\begin{pmatrix}0&0\\ 0&0\end{pmatrix}

Propiedades

Los divisores de cero por la izquierda o por la derecha nunca pueden ser unidades, porque, si a es invertible y ab = 0, entonces 0 = a-10 = a-1ab = b.

Todo elemento idempotente no nulo a≠1 es divisor de cero, ya que a² = a implica que a(a - 1) = (a - 1)a = 0. Los elementos nilpotentes no nulos del anillo también son divisores de cero triviales.

En el anillo de las matrices de n×n sobre algún campo, los divisores de cero por la izquierda y por la derecha coinciden; son precisamente las matrices singulares no nulas. En el anillo de las matrices de n×n sobre un dominio de integridad, los divisores de cero son precisamente las matrices no nulas de determinante cero.

Si a es un divisor de cero por la izquierda y x es un elemento arbitrario del anillo, entonces xa es cero o bien un divisor de cero. El siguiente ejemplo muestra que no se puede decir lo mismo de ax. Considérese el conjunto de matrices de ∞×∞ sobre el anillo de los enteros, donde cada fila y cada columna contiene un número finito de entradas no nulas. Éste es un anillo con el producto usual de matrices. La matriz

A = \begin{pmatrix} 0 & 1 & 0 &0&0&\\ 0 & 0 & 1 &0&0&\cdots\\ 0 & 0 & 0 &1&0&\\ 0&0&0&0&1&\\ &&\vdots&&&\ddots \end{pmatrix}

es un divisor de cero por la izquierda y B = AT es, por tanto, un divisor de cero por la derecha. Pero AB es la matriz identidad y, por tanto, no puede ser un divisor de cero. En particular, concluimos que A no puede ser un divisor de cero por la derecha.

Un anillo conmutativo con 0≠1 y sin divisores de cero recibe el nombre de dominio de integridad o dominio integral.

Obtenido de "Divisor de cero"

Wikimedia foundation. 2010.

Игры ⚽ Нужен реферат?

Mira otros diccionarios:

  • Divisor de cero — En álgebra abstracta, un elemento no nulo a de un anillo A es un divisor de cero por la izquierda si existe un elemento no nulo b tal que ab = 0. Los divisores de cero por la derecha se definen análogamente. Un elemento que es tanto un divisor de …   Enciclopedia Universal

  • Divisor — Saltar a navegación, búsqueda La palabra divisor, puede referirse a: Matemáticas Divisor (Divisibilidad) /Tabla de divisores Divisor aritmético Divisor de cero (Álgebra, anillos) el divisor es numero, que cuando se lo divide con un numero, su… …   Wikipedia Español

  • Cero — Para otros usos de este término, véase Cero (desambiguación). 0 Cardinal Cero Sistemas de numeración Ática O …   Wikipedia Español

  • Divisor — ► adjetivo/ sustantivo masculino 1 MATEMÁTICAS Se aplica al número que otro contiene dos o más veces exactamente: ■ el dos es el divisor de todos los números pares y de los terminados en cero. SINÓNIMO submúltiplo ► sustantivo masculino 2… …   Enciclopedia Universal

  • Divisor de tensión — Saltar a navegación, búsqueda Un divisor de tensión es una configuración de circuito eléctrico que reparte la tensión de una fuente entre una o más impedancias conectadas en serie. Supóngase que se tiene una fuente de tensión Vf, conectada en… …   Wikipedia Español

  • División por cero — Saltar a navegación, búsqueda Representación gráfica de la función y = 1/x. Cuando x «tiende» a 0+, y se «aproxima» a infinito. En matemáticas, la división por cero es aquella división en la que el divisor es igual …   Wikipedia Español

  • División por cero — En matemáticas, una división por cero es una división en la que el divisor es igual a cero. Es una operación no definida y puede llevar a paradojas matemáticas …   Enciclopedia Universal

  • Anillo (matemática) — En álgebra, un anillo es una estructura algebraica formada por un conjunto (A), y dos operaciones: suma y producto; de modo que (A,+) es un grupo conmutativo con elemento neutro (que designamos 0), y el producto es asociativo y tiene la propiedad …   Wikipedia Español

  • Característica (matemática) — Saltar a navegación, búsqueda En Álgebra abstracta, la característica de un anillo R es definida como el entero positivo más pequeño n tal que 1R+...+1R (con n sumandos) = 0. Si no existe tal n, decimos que la característica de R es 0. De forma… …   Wikipedia Español

  • División (matemática) — En matemática, la división es una operación aritmética de descomposición que consiste en averiguar cuántas veces un número (divisor) está contenido en otro número (dividendo). La división es la operación inversa de la multiplicación. Según su… …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”