División (matemática)

En matemática, la división es una operación aritmética de descomposición que consiste en averiguar cuántas veces un número (divisor) está contenido en otro número (dividendo). La división es la operación inversa de la multiplicación.

Según su resto, las divisiones se clasifican como exactas si su resto es cero o inexactas cuando no lo es.

Al resultado entero de la división se denomina cociente y si la división no es exacta, es decir, el divisor no está contenido un número exacto de veces en el dividendo, la operación tendrá un resto o residuo, donde:

Algoritmos para la división

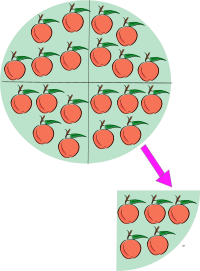
Ejemplo de una división.

El algoritmo de la división, también llamado división euclidiana, es un algoritmo que permite determinar el resultado de una divisón de números enteros, así como la existencia y unicidad del cociente y el residuo. Es utilizado además en otros métodos como el algoritmo de Euclides, para calcular el máximo común divisor de dos o más números enteros.

Se suele representar bajo el diagrama:

El algoritmo de la división se construye a partir de una tabla elemental, que es inversa de la de multiplicar.

La lectura de la tabla es, por ejemplo, 10 ÷ 5 = 2, leído: «diez entre cinco igual a dos» o, bien «diez dividido cinco es igual a dos».

División de números enteros

La división no es una operación cerrada, lo cual quiere decir que, en general, el resultado no será otro número entero, a menos que el dividendo sea un múltiplo entero del divisor. La divisón entre cero no está definida en matemáticas.

División de números racionales

El resultado de dividir dos fracciones es otra fracción (siempre y cuando el divisor no sea 0). Se puede definir de la manera siguiente: dados p/q and r/s,

Esta definición demuestra que la división es la operación inversa de la multiplicación.

División de números reales

El resultado de dividir dos números reales es otro número real (siempre y cuando el divisor no sea 0). Se define como a/b = c si y solo si a = cb y b ≠ 0.

División entre cero

La división de cualquier número por cero es una «indefinición». Esto resulta del hecho que cero multiplicado por cualquier cantidad finita es otra vez cero, es decir, que el cero no posee un inverso multiplicativo.

División de números complejos

El resultado de dividir dos números complejos es otro número complejo (siempre y cuando el divisor no sea 0). Se define como

en donde r y s ≠ 0.

En forma polar:

La división entre otros objetos matemáticos

División de monomios

Para dividir dos monomios se dividen sus coeficientes y se restan los exponentes de la parte literal. Si la división de los coeficientes no es exacta, se suele representar como fracción.

División de un polinomio por un monomio

Se divide cada término del polinomio por el monomio, separando los coeficientes parciales con sus propios signos.

División de polinomios

Regla para la división de dos polinomios:

1. Se ordenan los polinomios dados con respecto a una letra. Si falta algún término para ordenar el dividendo, se deja el espacio o se pone cero.
2. Se divide el primer término del dividendo entre el primer término del divisor.
3. Se multiplica este cociente por cada término del divisor y este producto se resta del dividendo.
4. A la diferencia obtenida se le agrega el siguiente término del dividendo y se repite la operación hasta que se hayan dividido todos los términos del dividendo.

Existen otros algoritmos para dividir polinomios, como el de Horner, el de Ruffini o el teorema del resto. Algunos de estos métodos sólo son aplicables a ciertos tipos de polinomios.

Criterios de divisibilidad

• Un número es divisible por 2 si es par (su última cifra es 2, 4, 6, 8 ó 0).
• Un número es divisible por 3 si la suma de sus cifras es múltiplo de 3.
• Un número es divisible por 4 si el número formado por las últimas dos cifras es múltiplo de 4 o termina en doble 0.
• Un número es divisible por 5 si termina en 0 o en 5.
• Un número es divisible por 6 si es divisible por 2 y 3.
• Un número es divisible por 7 cuando la diferencia entre el número sin la cifra de las unidades y el doble de la cifra de las unidades es cero o múltiplo de 7.
• Un número es divisible por 8 si el número formado por las últimas tres cifras es múltiplo de 8.
• Un número es divisible por 9 si la suma de sus cifras es múltiplo de 9.
• Un número es divisible por 10 si termina en 0.
• Un número es divisible por 11 cuando la diferencia entre la suma de los valores absolutos de las cifras de los lugares pares y la suma de los valores absolutos de los lugares impares, en el sentido posible, es múltiplo de 11.
• Un número es divisible por 12 si es divisible por 3 y 4.

Estos criterios sirven en particular para descomponer los enteros en factores primos, lo que se usa en cálculos como el mínimo común múltiplo o el máximo común divisor.

Véase también

• Wikiquote alberga frases célebres de o sobre División (matemática). Wikiquote
• Divisibilidad
• División por cero
• Algoritmo de la división

Referencias

• «dividir», Diccionario de la lengua española (vigésima segunda edición), Real Academia Española, 2001, http://buscon.rae.es/draeI/SrvltConsulta?TIPO_BUS=3&LEMA=dividir 
• Weisstein, Eric W. "Division." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/Division.html

Enlaces externos

• Matemáticas en la BBC
• Ejemplos de divisiones (Álgebra)