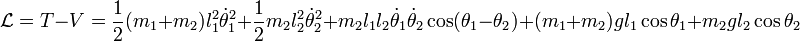- Doble péndulo
-
Doble péndulo
En general, un doble péndulo es un sistema compuesto por dos péndulos, con el segundo colgando del extremo del primero. En el caso más simple, se trata de dos péndulos simples, con el inferior colgando de la masa pendular del superior.
Normalmente se sobreentiende que nos referimos a un doble péndulo plano, con dos péndulos planos coplanarios. Este sistema físico posee dos grados de libertad y exhibe un rico comportamiento dinámico. Su movimiento está gobernado por dos ecuaciones diferenciales ordinarias acopladas. Por encima de cierta energía, su movimiento es caótico.
Contenido
Análisis del movimiento del péndulo doble plano
Cinemática
En la cinemática sólo estamos interesados en encontrar las expresiones de la posición, la velocidad, la aceleración y en términos de las variables que especifican el estado del doble péndulo, sin interesarnos por las fuerzas actuantes. Nos serviremos de las siguientes coordenadas:
- x,y = posición horizontal y vertical de la masa de un péndulo
- θ = ángulo de un péndulo respecto a la vertical (0 = vertical hacia abajo, antihorario es positivo)
- l = longitud de la varilla (constante)
Asociaremos al péndulo superior el subíndice 1, y al de abajo el subíndice 2. Pondremos el origen de coordenadas en el punto de pivote del péndulo superior. El sentido de las ordenadas crecientes se toma hacia arriba.
A partir de consideraciones trigonométricas escribimos las expresiones de las posiciones x1, y1, x2, y2 en términos de los ángulos θ1, θ2:
Derivando con respecto al tiempo obtenemos:
Y derivando una segunda vez:
Fuerzas
Definimos las variables:
- T = tensión en la varilla
- M = masa del péndulo
- g = constante gravitacional
Usaremos la ley de Newton F = ma, escribiendo por separado las ecuaciones de las componentes verticales y horizontales de las fuerzas.
Sobre la masa m1 actúan la tensión en la parte superior de la varilla T1, la tensión en la parte inferior de la varillaT2, y la gravedad -m1g:
Sobre la masa m2, actúan la tensión T2 y la gravedad –m2g:
Ecuaciones de movimiento
A parttir de las ecuaciones anteriores, tras realizar numerosas operaciones algebraicas con la finalidad de encontrar las expresiones de
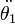 ,
, 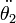 en términos de
en términos de 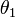 ,
, 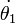 ,
, 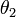 ,
, 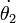 , llegaríamos a las ecuaciones de movimiento para el péndulo doble:
, llegaríamos a las ecuaciones de movimiento para el péndulo doble:Energía
La energía cinética viene expresada por:
La energía potencial :
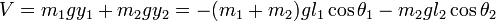 .
.
Por tanto, el movimiento se regirá por la lagrangiana
Véase también
- Péndulo
- Péndulo balístico
- Péndulo cicloidal
- Péndulo cónico
- Péndulo de Foucault
- Péndulo de Newton
- Péndulo de Pohl
- Péndulo de torsión
- Péndulo esférico
- Péndulo físico
- Péndulo simple
- Péndulo simple equivalente
Referencias
Bibliografía
- Marion, Jerry B. (1996). Dinámica clásica de las partículas y sistemas (en español). Barcelona: Ed. Reverté. ISBN 84-291-4094-8.
Enlaces externos
- Artículo en scienceworld de Eric Weisstein (en inglés).
- Animación que muestra movimiento del péndulo doble y reparto de energía entre uno y otro péndulo
- Curso Interactivo de Física en Internet. Ángel Franco García.
Categorías: Física | Mecánica | Dinámica | Péndulo
Wikimedia foundation. 2010.


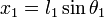
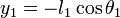
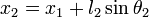
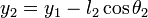
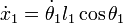
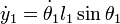
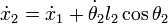
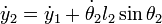
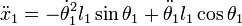
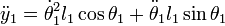
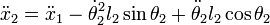
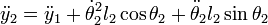
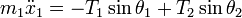
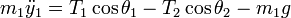
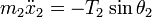
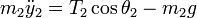
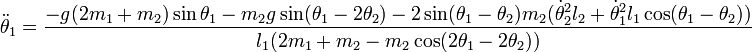
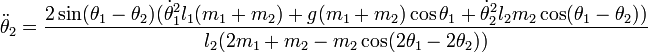
![T=\frac{1}{2}m_1(\dot x_1^2+\dot y_1^2)+\frac{1}{2}m_2(\dot x_2^2+\dot y_2^2)=
\frac{1}{2}m_1l_1^2\dot{\theta}_1^2 +
\frac{1}{2}m_2[l_1^2\dot{\theta}_1^2+l_2^2\dot{\theta}_2^2 +
2l_1l_2\dot{\theta}_1\dot{\theta}_2\cos(\theta_1-\theta_2)]](/pictures/eswiki/51/36a894b052f59175b2c03aa0b3715f1c.png)