- Péndulo de Kater
-
Péndulo de Kater
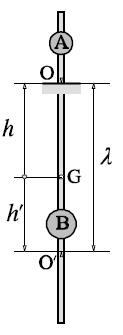 Péndulo de Kater (esquema)
Péndulo de Kater (esquema)
Contenido
Definición
El péndulo de Kater es un péndulo reversible inventado por el capitán de la armada británica Henry Kater en 1817 como un instrumento gravimétrico destinado a medir la aceleración gravitatoria local. Su ventaja, con respecto a anteriores métodos gravimétrico que utilizaban péndulos, radica que que no es necesario determinar ni el centro de gravedad ni el centro de oscilación del péndulo, lo que permite una gran precisión. Durante poco más de una centuria, hasta la década de 1930, el péndulo de Kater, y sus sucesivas mejoras, constituyó el método estándar para la medida de la intensidad gravitatoria en las prospecciones geodésicas. Hodierno tan sólo es utilizado para demostraciones docentes de los principios del péndulo.
Descripción
El péndulo de Kater es un péndulo compuesto que está formado por una barra metálica rígida provista de dos cuchillas (O y O′), con sus bordes enfrentados, como se indica en la Figura. Las cuchillas, apoyadas por sus bordes sobre un soporte rígido y robusto, sirven como centros (ejes) de suspensión. Dos discos metálicos (A y B) pueden desplazarse a lo largo de la barra del péndulo. El disco de menor masa (A) está situado en uno de los extremos de la barra, fuera de las cuchillas; el otro (B), más pesado, está colocado entre las cuchillas.
Ajustando convenientemente las posiciones de las masas deslizantes sobre la barra del péndulo, puede conseguirse que sean iguales los periodos de oscilación del péndulo cuando está suspendido de la cuchilla O o de la cuchilla O′; en estas condiciones, los puntos O y O′ son conjugados y la distancia que los separa es la [[longitud reducida]] λ del péndulo. En consecuencia, podemos determinar el valor de la intensidad del campo gravitatorio, g, a partir de la expresión:
Medida de g. Método de Bessel
Friedrich Bessel demostró que, para la determinación exacta del valor de g no es necesario el lento proceso que nos llevaría a conseguir que los dos periodos de oscilación, T y T′, sean exactamente iguales. Es suficiente que sean aproximadamente iguales, i.e., que la diferencia T-T′ sea muy pequeña.
En efecto, a partir de una de las expresiones del periodo del péndulo compuesto,
en la que K es el radio de giro con respecto a un eje paralelo al de suspensión que pase por el centro de gravedad G del péndulo y h es la distancia OG, podemos obtener:
de modo que, restando miembro a miembro, tenemos:
de donde
Entonces, si el centro de gravedad (G) del péndulo se encuentra más cerca de una cuchilla que de la otra, la diferencia (h-h′) no es pequeña y, puesto que T es aproximadamente igual a T′, el segundo término de la expresión anterior será despreciable en comparación con el primero, por lo que el valor de g puede obtenerse mediante la fórmula:
Véase también
- Péndulo
- Péndulo balístico
- Péndulo cicloidal
- Péndulo compuesto
- Péndulo cónico
- Péndulo de Foucault
- Péndulo de Foucault (lista)
- Péndulo de Newton
- Péndulo de Pohl
- Péndulo de torsión
- Péndulo esférico
- Péndulo físico
- Péndulo simple
- Péndulo simple equivalente
- Reloj de péndulo
- Teorema de Huygens
- Oscilador armónico
- Oscilador armónico
- Doble péndulo
- Metrónomo
Referencias
Bibliografía
- Feynman, Leighton and Sands. Lectures on physics. Addison-Wesley. ISBN 0-8053-9045-6.
- Marion, Jerry B. (1996). Dinámica clásica de las partículas y sistemas. Barcelona: Ed. Reverté. ISBN 84-291-4094-8.
- Ortega, Manuel R. (1989-2006). Lecciones de Física (4 volúmenes). Monytex. ISBN 84-404-4290-4, ISBN 84-398-9218-7, ISBN 84-398-9219-5, ISBN 84-604-4445-7.
- Tipler, Paul A. (2000). Física para la ciencia y la tecnología (2 volúmenes). Barcelona: Ed. Reverté. ISBN 84-291-4382-3.
- Resnick,R. and Halliday, D. (1996). Physics. John Wiley & Sons. ISBN 0-471-83202-2.
Referencias externas
- Física Universitaria. (en español) Abundante información para el nivel de la Física Universitaria. Incluye textos y animaciones.
- Curso Interactivo de Física en Internet. Ángel Franco García.
- Página en inglés Con animaciones de oscilaciones y ondas.
Categorías: Física | Mecánica | Oscilaciones | Péndulo
Wikimedia foundation. 2010.


![T = 2\pi \sqrt{{\lambda\over g}} \qquad \Rightarrow \qquad g = 4 {\pi}^2{\lambda \over T} \qquad\qquad [1]](/pictures/eswiki/99/caf91d47a71a4496ece7f2b8dda94404.png)
![T = 2 \pi \sqrt{{h^2+K^2}\over gh} \qquad\qquad [2]](/pictures/eswiki/99/c1a9ae1771345b0189d1394ffac3cb35.png)
![{ghT^2 \over 4\pi^2} = h^2+K^2 \qquad \text{y} \qquad {gh'T'^2 \over 4\pi^2} = h'^2+K^2 \qquad\qquad [3]](/pictures/eswiki/102/fdfda366b15b7de3a9ecac9c23905c60.png)
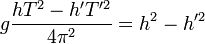
![{4\pi^2 \over g} = {hT^2 - h'T'^2 \over h^2-h'^2} = {T^2 + T'^2 \over 2(h+h')} + {T^2 - T'^2 \over 2(h-h')} \qquad\qquad [4]](/pictures/eswiki/50/255747f364d2b154650e325bf56f0ce5.png)
![g = 8\pi^2 {h+h' \over T^2+T'^2} \qquad\qquad [5]](/pictures/eswiki/55/7c0e4741a5c328ca99c24e78aed3f66d.png)