Péndulo cónico

Péndulo cónico

Péndulo cónico

El péndulo cónico está constituido por un cuerpo pesado de pequeñas dimensiones (puntual, idealmente) suspendido de un punto fijo mediante un hilo inextensible y de masa despreciable. Su construcción es la misma que la de un péndulo simple, pero, a diferencia de éste, el péndulo cónico no oscila, sino que la masa pendular describe una trayectoria circular en un plano horizontal con aceleración constante. Su nombre proviene del hecho de que el hilo traza una superficie cónica.

El científico inglés Robert Hooke fue el primero en estudiar las características de este péndulo, en 1660.

Péndulo coníco.

El péndulo cónico consiste en una masa de pequeñas dimensiones supendida de un punto fijo mediante un hilo inextensible y de masa despreciable, de modo que la masa pendular se mueve en un plano horizontal describiendo una trayectoría circular. Su nombre poviene del hecho de que el hilo de suspensión gerera una superficie cónica.

El péndulo cónico es un caso particular del péndulo esférico.

Contenido

Análisis del movimiento

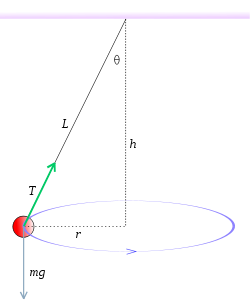
Consideremos un péndulo cónico consistente en una pequeña esfera de masa m que se mueve sin fricción en una circunferencia horizontal con una celeridad constante v, suspendida de un hilo de longitud L que forma un ángulo constante θ con la vertical.

Sobre la masa m actúan dos fuerzas: su propio peso, mg, y la tensión del hilo, T.

La componente horizontal de la tensión del hilo proporciona la aceleración centrípeta, 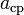a_\text{cp}\,\;, asociada con el movimiento circular. La componente vertical de la tensión se compensa exactamente con el peso de la masa m. La aplicación de la segunda ley de Newton en las direcciones horizontal y vertical nos permite escribir:

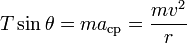
(1) T \sin \theta = ma_\text{cp} = \frac {mv^2}{r} \,

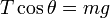
(2) T \cos \theta = mg \,

Dividiendo miembro a miembros estas dos ecuaciones, eliminamos T y m, resultando:

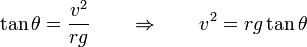
(3) \tan\theta=\frac{v^2}{rg} \qquad\Rightarrow\qquad v^2=rg\tan\theta

Puesto que la celeridad v es constante, puede expresarse en función del tiempo 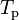T_\text{p}\, requerido para realizar una revolución completa o periodo de revolución,

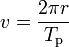
(4) v = \frac {2\pi r}{T_\text{p} }

y sustituyendo en la ecuación (3), después de fáciles operaciones, obtenemos:

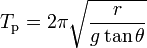
(5) T_\text{p} = 2 \pi \sqrt {\frac {r} {g \tan \theta}}

En la ejecución práctica de la experiencia, r varía y no es estan fácil de medir como la longitud constante L del hilo. Recurriendo a la relación trigonométria entre r, h, y L, esto es, 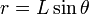r = L \sin \theta \,, la relación (5) se escribe en la forma:

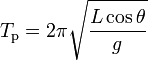
(6) T_\text{p} = 2 \pi \sqrt { \frac {L \cos \theta} {g} }

Para pequeños ángulos será cos(θ) ≈ 1 y el periodo de revolución del péndulo cónico resulta ser casi igual al periodo de oscilación del péndulo simple de la misma longitud. Además, para pequeños ángulos, el periodo de revolución es aproximadamente independiente del valor del ángulo θ, lo que significa que, a pesar de que el ángulo vaya disminuyendo (por frición con el aire, por ejemplo), el periodo permanece prácticamente constante. Esta propiedad, llamada isocronismo, la poseen también los péndulos ordinarios.

Véase también

Referencias

Bibliografía

  • Ortega, Manuel R. (1989-2006). Lecciones de Física (4 volúmenes) (en español). Monytex. ISBN 84-404-4290-4, ISBN 84-398-9218-7, ISBN 84-398-9219-5, ISBN 84-604-4445-7.
  • Resnick, Robert & Halliday, David (2004). Física 4ª (en español). CECSA, México. ISBN 970-24-0257-3.
  • Serway, Raymond A.; Jewett, John W. (2004). Physics for Scientists and Engineers, 6ª edición (en inglés), Brooks/Cole. ISBN 0-534-40842-7.
  • Tipler, Paul A. (2000). Física para la ciencia y la tecnología (2 volúmenes) (en español). Barcelona: Ed. Reverté. ISBN 84-291-4382-3.

Enlaces externos

Véase también

Referencias

Bibliografía

  • Ortega, Manuel R. (1989-2006). Lecciones de Física (4 volúmenes) (en español). Monytex. ISBN 84-404-4290-4, ISBN 84-398-9218-7, ISBN 84-398-9219-5, ISBN 84-604-4445-7.
  • Resnick,Robert & Krane, Kenneth S. (2001). Physics (en inglés). New York: John Wiley & Sons.
  • Serway, Raymond A.; Jewett, John W. (2004). Physics for Scientists and Engineers, 6ª edición (en inglés), Brooks/Cole. ISBN 0-534-40842-7.
  • Tipler, Paul A. (2000). Física para la ciencia y la tecnología (2 volúmenes) (en español). Barcelona: Ed. Reverté. ISBN 84-291-4382-3.

Enlaces externos

Obtenido de "P%C3%A9ndulo c%C3%B3nico"

Wikimedia foundation. 2010.

Игры ⚽ Нужно сделать НИР?

Mira otros diccionarios:

  • Péndulo — Saltar a navegación, búsqueda Para otros usos de este término, véase Péndulo (desambiguación). El péndulo (del lat. pendŭlus, pendiente) es un sistema físico que puede oscilar bajo la acción gravitatoria u otra caraterística física (elasticidad,… …   Wikipedia Español

  • Péndulo físico — Saltar a navegación, búsqueda Un péndulo físico o compuesto es cualquier cuerpo rígido que pueda oscilar libremente en el campo gravitatorio alrededor de un eje horizontal fijo, que no pasa por su centro de masa. Contenido 1 Deducción del periodo …   Wikipedia Español

  • Péndulo de Foucault — Saltar a navegación, búsqueda Para la novela de Umberto Eco, véase El péndulo de Foucault. Animación del péndulo de Foucault Un péndulo de Foucault es un péndulo esférico que puede oscilar libremente en cualquier plano vertical y capaz de oscilar …   Wikipedia Español

  • Péndulo de Kater — Saltar a navegación, búsqueda Péndulo de Kater original (tomado de una publicación de Kater de 1818) …   Wikipedia Español

  • Péndulo simple — Saltar a navegación, búsqueda El péndulo simple o matemático es un sistema idealizado constituido por una partícula de masa m que está suspendida de un punto fijo O mediante un hilo inextensible y sin peso. Naturalmente es imposible la… …   Wikipedia Español

  • Péndulo cicloidal — Saltar a navegación, búsqueda Las oscilaciones del péndulo simple sólo son isócronas para pequeñas amplitudes. Sin embargo, existe un diseño especial en el que el periodo es independiente de la amplitud; se trata del péndulo cicloidal, llamado… …   Wikipedia Español

  • Péndulo balístico — Saltar a navegación, búsqueda Péndulo balístico Un péndulo balístico es un dispositivo permite determinar la velocidad de un proyectil. Este péndulo está constituido por un bloque grande de madera, de masa M, suspendido mediant …   Wikipedia Español

  • Péndulo de torsión — Saltar a navegación, búsqueda El péndulo de torsión consiste en un hilo o alambre de sección recta circular suspendido verticalmente, con su extremo superior fijo. En el extremo inferior del hilo se cuelga un cuerpo de momento de inercia I… …   Wikipedia Español

  • Doble péndulo — Saltar a navegación, búsqueda Para otros usos de este término, véase Péndulo (desambiguación). En general, un doble péndulo es un sistema compuesto por dos péndulos, con el segundo colgando del extremo del primero. En el caso más simple, se trata …   Wikipedia Español

  • Gabriel Galán Ruiz — Este artículo o sección necesita referencias que aparezcan en una publicación acreditada, como revistas especializadas, monografías, prensa diaria o páginas de Internet fidedignas. Puedes añadirlas así o avisar …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”