Péndulo esférico

Péndulo esférico

Péndulo esférico

Péndulo esférico animado

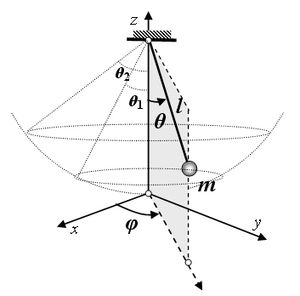
El péndulo esférico es una variante del péndulo simple en el que el movimiento de la masa pendular está confinado al segmento esférico delimitado entre dos paralelos. En consecuencia, es un sistema con dos grados de libertad.

Contenido

Fundamento teórico

Existen dos integrales o constantes de movimiento: la energía E y la componente del momento angular paralela al eje vertical Mz. La función lagrangiana viene dada por:

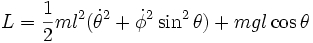
L = \frac{1}{2}ml^2(\dot{\theta}^2+ \dot{\phi}^2\sin^2\theta)+mgl\cos\theta

donde φ es el ángulo polar y θ es el ángulo que forma el hilo o barra del péndulo con la vertical. Las ecuaciones de movimiento, obtenidas introduciendo el lagrangiano anterior en las ecuaciones de Euler-Lagrange son:

Diagrama ilustrativo del péndulo esférico

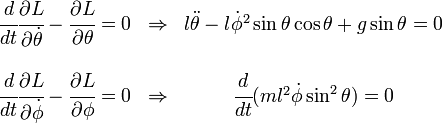
\begin{matrix} \cfrac{d}{dt}\cfrac{\part L}{\part\dot\theta} - \cfrac{\part L}{\part\theta}=0 &\Rightarrow & l\ddot\theta - l\dot{\phi}^2\sin\theta\cos\theta + g \sin\theta = 0 \\ \\ \cfrac{d}{dt}\cfrac{\part L}{\part\dot\phi} - \cfrac{\part L}{\part\phi}=0 &\Rightarrow & \cfrac{d}{dt}(ml^2\dot{\phi}\sin^2\theta) = 0 \end{matrix}

La segunda ecuación expresa la constancia de la componente Z del momento angular y lleva a la relación entre la velocidad de giro polar y el momento angular

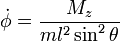
\dot\phi = \frac{M_z}{ml^2\sin^2\theta}

Así, podemos reescribir la lagrangiana como:

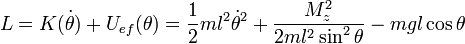
L = K(\dot\theta)+ U_{ef}(\theta) = \frac{1}{2}ml^2\dot{\theta}^2 + \frac{M_z^2}{2ml^2\sin^2\theta}-mgl\cos\theta

de modo que el problema queda reducido a un problema unidimensional.

Período

El movimiento de un péndulo esférico en general no es periódico, ya que resulta de la combinación de dos movimientos periódicos de períodos generalmente incomensurables. Sin embargo el movimiento resulta cuasiperiódico; esto es, observadas una posición y una velocidad en el movimiento, existe un tiempo T tal que el péndulo estará a una distancia tan pequeña como se desee de esa posición y tendrá una velocidad tan parecida como se quiera, pero sin repetirse exactamente. Dado que la región de movimiento es compacta, el conjunto de puntos de la trayectoria de un péndulo esférico constituye un conjunto denso sobre una área esférica comprendida entre dos casquetes esféricos.

Solución de la ecuación de movimiento

Las ecuaciones de movimiento pueden expresarse en términos de integrales elípticas de primera especie y tercera especie:

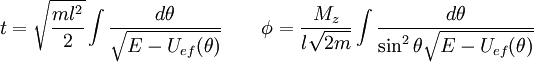
t = \sqrt\frac{ml^2}{2} \int \frac{d\theta}{\sqrt{E-U_{ef}(\theta)}} \qquad \phi = \frac{M_z}{l\sqrt{2m}} \int \frac{d\theta}{\sin^2\theta\sqrt{E-U_{ef}(\theta)}}

Referencias

Véase también

Bibliografía

  • Marion, Jerry B. (1996). Dinámica clásica de las partículas y sistemas (en español). Barcelona: Ed. Reverté. ISBN 84-291-4094-8.
  • Daw H. A., Coriolis lecture demostration. Am. J. Phys. 55 (11) November 1987, pp. 1010-1014

Enlaces externos

Obtenido de "P%C3%A9ndulo esf%C3%A9rico"

Wikimedia foundation. 2010.

Игры ⚽ Поможем сделать НИР

Mira otros diccionarios:

  • Péndulo — Saltar a navegación, búsqueda Para otros usos de este término, véase Péndulo (desambiguación). El péndulo (del lat. pendŭlus, pendiente) es un sistema físico que puede oscilar bajo la acción gravitatoria u otra caraterística física (elasticidad,… …   Wikipedia Español

  • Péndulo cónico — Saltar a navegación, búsqueda El péndulo cónico está constituido por un cuerpo pesado de pequeñas dimensiones (puntual, idealmente) suspendido de un punto fijo mediante un hilo inextensible y de masa despreciable. Su construcción es la misma que… …   Wikipedia Español

  • Péndulo de Foucault — Saltar a navegación, búsqueda Para la novela de Umberto Eco, véase El péndulo de Foucault. Animación del péndulo de Foucault Un péndulo de Foucault es un péndulo esférico que puede oscilar libremente en cualquier plano vertical y capaz de oscilar …   Wikipedia Español

  • Péndulo físico — Saltar a navegación, búsqueda Un péndulo físico o compuesto es cualquier cuerpo rígido que pueda oscilar libremente en el campo gravitatorio alrededor de un eje horizontal fijo, que no pasa por su centro de masa. Contenido 1 Deducción del periodo …   Wikipedia Español

  • Péndulo de Kater — Saltar a navegación, búsqueda Péndulo de Kater original (tomado de una publicación de Kater de 1818) …   Wikipedia Español

  • Péndulo simple — Saltar a navegación, búsqueda El péndulo simple o matemático es un sistema idealizado constituido por una partícula de masa m que está suspendida de un punto fijo O mediante un hilo inextensible y sin peso. Naturalmente es imposible la… …   Wikipedia Español

  • Péndulo cicloidal — Saltar a navegación, búsqueda Las oscilaciones del péndulo simple sólo son isócronas para pequeñas amplitudes. Sin embargo, existe un diseño especial en el que el periodo es independiente de la amplitud; se trata del péndulo cicloidal, llamado… …   Wikipedia Español

  • Péndulo balístico — Saltar a navegación, búsqueda Péndulo balístico Un péndulo balístico es un dispositivo permite determinar la velocidad de un proyectil. Este péndulo está constituido por un bloque grande de madera, de masa M, suspendido mediant …   Wikipedia Español

  • Péndulo de torsión — Saltar a navegación, búsqueda El péndulo de torsión consiste en un hilo o alambre de sección recta circular suspendido verticalmente, con su extremo superior fijo. En el extremo inferior del hilo se cuelga un cuerpo de momento de inercia I… …   Wikipedia Español

  • Péndulo (desambiguación) — Saltar a navegación, búsqueda El término péndulo puede hacer referencia a: Péndulo, un sistema físico ideal constituido por un hilo inextensible y de masa despreciable, sostenido por su extremo superior de un punto fijo, con una masa puntual en… …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”