Principio de Bernoulli

Principio de Bernoulli
Para el teorema matemático enunciado por Jakob Bernoulli, véase Teorema de Bernoulli.
Esquema del Principio de Bernoulli.

El principio de Bernoulli, también denominado ecuación de Bernoulli o Trinomio de Bernoulli, describe el comportamiento de un fluido moviéndose a lo largo de una línea de corriente. Fue expuesto por Daniel Bernoulli en su obra Hidrodinámica (1738) y expresa que en un fluido ideal (sin viscosidad ni rozamiento) en régimen de circulación por un conducto cerrado, la energía que posee el fluido permanece constante a lo largo de su recorrido. La energía de un fluido en cualquier momento consta de tres componentes:

  1. Cinética: es la energía debida a la velocidad que posea el fluido.
  2. Potencial gravitacional: es la energía debido a la altitud que un fluido posea.
  3. Energía de flujo: es la energía que un fluido contiene debido a la presión que posee.

La siguiente ecuación conocida como "Ecuación de Bernoulli" (Trinomio de Bernoulli) consta de estos mismos términos.

\frac{V^2 \rho}{2}+{P}+{\rho g z}=constante

donde:

  • V = velocidad del fluido en la sección considerada.
  • ρ = densidad del fluido.
  • P = presión a lo largo de la línea de corriente.
  • g = aceleración gravitatoria
  • z = altura en la dirección de la gravedad desde una cota de referencia.

Para aplicar la ecuación se deben realizar los siguientes supuestos:

  • Viscosidad (fricción interna) = 0 Es decir, se considera que la línea de corriente sobre la cual se aplica se encuentra en una zona 'no viscosa' del fluido.
  • Caudal constante
  • Flujo incompresible, donde ρ es constante.
  • La ecuación se aplica a lo largo de una línea de corriente o en un flujo irrotacional

Aunque el nombre de la ecuación se debe a Bernoulli, la forma arriba expuesta fue presentada en primer lugar por Leonhard Euler.

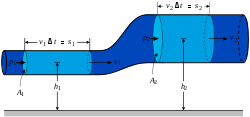
Un ejemplo de aplicación del principio lo encontramos en el flujo de agua en tubería.

Contenido

Características y consecuencias

Cada uno de los términos de esta ecuación tiene unidades de longitud, y a la vez representan formas distintas de energía; en hidráulica es común expresar la energía en términos de longitud, y se habla de altura o cabezal, esta última traducción del inglés head. Así en la ecuación de Bernoulli los términos suelen llamarse alturas o cabezales de velocidad, de presión y cabezal hidráulico, del inglés hydraulic head; el término z se suele agrupar con P / γ para dar lugar a la llamada altura piezométrica o también carga piezométrica.

\overbrace{{V^2 \over 2 g}}^{\mbox{cabezal de velocidad}}+\overbrace{\underbrace{\frac{P}{\gamma}}_{\mbox{cabezal de presión}} + z}^{\mbox{altura o carga piezométrica}} = \overbrace{H}^{\mbox{Cabezal o Altura hidráulica}}

También podemos reescribir este principio en forma de suma de presiones multiplicando toda la ecuación por γ, de esta forma el término relativo a la velocidad se llamará presión dinámica, los términos de presión y altura se agrupan en la presión estática.

Esquema del efecto Venturi.
\underbrace{\frac{\rho V^2}{2}}_{\mbox{presión dinámica}}+\overbrace{P+ \gamma z}^{\mbox{presión estática}}=constante

o escrita de otra manera más sencilla:

q + p = p0

donde

  • q=\frac{\rho V^2}{2}
  • p = P + γz
  • p0 es una constante-

Igualmente podemos escribir la misma ecuación como la suma de la energía cinética, la energía de flujo y la energía potencial gravitatoria por unidad de masa:

\overbrace{\frac{{V}^2}{2}}^{\mbox{energía cinética}}+\underbrace{\frac{P}{\rho}}_{\mbox{energía de flujo}}+\overbrace{g z}^{\mbox{energía potencial}} = constante

Así el principio de bernoulli puede ser visto como otra forma de la ley de la conservación de la energía, es decir, en una línea de corriente cada tipo de energía puede subir o disminuir en virtud de la disminución o el aumento de las otras dos.

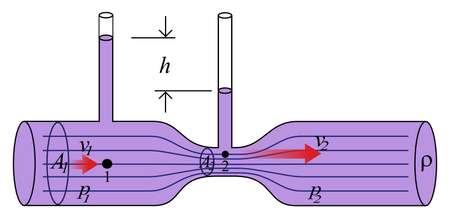
Esta ecuación permite explicar fenómenos como el efecto Venturi, ya que la aceleración de cualquier fluido en un camino equipotencial (con igual energía potencial) implicaría una disminución de la presión. Este efecto explica porqué las cosas ligeras muchas veces tienden a salirse de un automóvil en movimiento cuando se abren las ventanas. La presión del aire es menor fuera debido a que está en movimiento respecto a aquél que se encuentra dentro, donde la presión es necesariamente mayor. De forma, aparentemente, contradictoria el aire entra al vehículo pero esto ocurre por fenómenos de turbulencia y capa límite.

Ecuación de Bernoulli y la Primera Ley de la Termodinámica

De la primera ley de la termodinámica se puede concluir una ecuación estéticamente parecida a la ecuación de Bernouilli anteriormente señalada, pero conceptualmente distinta. La diferencia fundamental yace en los límites de funcionamiento y en la formulación de cada fórmula. La ecuación de Bernoulli es un balance de fuerzas sobre una partícula de fluido que se mueve a través de una línea de corriente, mientras que la primera ley de la termodinámica consiste en un balance de energía entre los límites de un volumen de control dado, por lo cual es más general ya que permite expresar los intercambios energéticos a lo largo de una corriente de fluido, como lo son las pérdidas por fricción que restan energía, y las bombas o ventiladores que suman energía al fluido. La forma general de esta, llamémosla, "forma energética de la ecuación de Bernoulli" es:

\frac{{V_1}^2}{2 g}+\frac{P_1}{\gamma}+z_1\frac{g}{g_c}+ W = h_f + \frac{{V_2}^2}{2 g}+\frac{P_2}{\gamma}+z_2\frac{g}{g_c}

donde:

  • γ es el peso específico (γ = ρg).
  • W es una medida de la energía que se le suministra al fluido.
  • hf es una medida de la energía empleada en vencer las fuerzas de fricción a través del recorrido del fluido.
  • Los subíndices 1 y 2 indican si los valores están dados para el comienzo o el final del volumen de control respectivamente.
  • g = 9,81 m/s2 y gc = 1 kg·m/(N·s2)

Suposiciones

La ecuación arriba escrita es un derivado de la primera ley de la termodinámica para flujos de fluido con las siguientes características.

  • El fluido de trabajo, es decir, aquél que fluye y que estamos considerando, tiene una densidad constante.
  • No existe cambio de energía interna.

Demostración

Escribamos la primera ley de la termodinámica con un criterio de signos termodinámico conveniente:

w + q = \Delta h + \Delta \frac{V^2}{2} + g \Delta z

Recordando la definición de la entalpía h = u + Pv, donde u es la energía interna y v se conoce como volumen específico v = 1 / ρ. Podemos escribir:

w + q = \Delta u + \Delta \frac{P}{\rho} + \Delta \frac{V^2}{2} + g \Delta z

que por la suposiciones declaradas más arriba se puede reescribir como:

w + q = \frac{P_2}{\rho} - \frac{P_1}{\rho} + \frac{{V_2}^2}{2} - \frac{{V_1}^2}{2} + g (z_2 - z_1)

dividamos todo entre el término de la aceleración de gravedad

\frac{w}{g} + \frac{q}{g} = \frac{P_2}{\gamma} - \frac{P_1}{\gamma} + \frac{{V_2}^2}{2 g} - \frac{{V_1}^2}{2 g} + z_2 - z_1

Los términos del lado izquierdo de la igualdad son relativos a los flujos de energía a través del volumen de control considerado, es decir, son las entradas y salidas de energía del fluido de trabajo en formas de trabajo (w) y calor (q). El término relativo al trabajo w / g consideraremos que entra al sistema, lo llamaremos h y tiene unidades de longitud, al igual que q / g, que llamaremos hf quién sale del sistema, ya que consideraremos que sólo se intercambia calor por vía de la fricción entre el fluido de trabajo y las paredes del conducto que lo contiene. Así la ecuación nos queda:

h -h_f= \frac{P_2}{\gamma} - \frac{P_1}{\gamma} + \frac{{V_2}^2}{2 g} - \frac{{V_1}^2}{2 g} + z_2 - z_1

o como la escribimos originalmente:

\frac{{V_1}^2}{2 g}+\frac{P_1}{\gamma}+z_1 + h = h_f + \frac{{V_2}^2}{2 g}+\frac{P_2}{\gamma}+z_2

Así, podemos observar que el principio de Bernoulli es una consecuencia directa de la primera ley de la termodinámica, o si se quiere, otra forma de esta ley. En la primera ecuación presentada en este artículo el volumen de control se había reducido a tan solo una línea de corriente sobre la cual no habían intercambios de energía con el resto del sistema, de aquí la suposición de que el fluido debería ser ideal, es decir, sin viscosidad ni fricción interna, ya que no existe un término hf entre las distintas líneas de corriente.

Aplicaciones del Principio de Bernoulli

Chimenea
Las chimeneas son altas para aprovechar que la velocidad del viento es más constante y elevada a mayores alturas. Cuanto más rápidamente sopla el viento sobre la boca de una chimenea, más baja es la presión y mayor es la diferencia de presión entre la base y la boca de la chimenea, en consecuencia, los gases de combustión se extraen mejor.

Tubería
La ecuación de Bernoulli y la ecuación de continuidad también nos dicen que si reducimos el área transversal de una tubería para que aumente la velocidad del fluido que pasa por ella, se reducirá la presión.

Natación
La aplicación dentro de este deporte se ve reflejado directamente cuando las manos del nadador cortan el agua generando una menor presión y mayor propulsión.

Carburador de automóvil
En un carburador de automóvil, la presión del aire que pasa a través del cuerpo del carburador, disminuye cuando pasa por un estrangulamiento. Al disminuir la presión, la gasolina fluye, se vaporiza y se mezcla con la corriente de aire.

Flujo de fluido desde un tanque
La tasa de flujo está dada por la ecuación de Bernoulli.

Dispositivos de Venturi
En oxigenoterapia, la mayor parte de sistemas de suministro de débito alto utilizan dispositivos de tipo Venturi, el cual esta basado en el principio de Bernoulli.

Véase también


Wikimedia foundation. 2010.

Игры ⚽ Нужна курсовая?

Mira otros diccionarios:

  • principio de Bernoulli — (en física) principio que afirma que la suma de la velocidad y la energía cinética de un líquido que fluye a través de un tubo es constante. Cuanto mayor es la velocidad, menor es la presión lateral en la pared …   Diccionario médico

  • Principio de Bernoulli — Este principio físico no debe confundirse con el Teorema de Bernoulli, de ámbito matemático Daniel Bernoulli, en su obra Hidrodinámica (1738) expuso este principio, que expresa que, en un fluido perfecto (sin viscosidad, ni rozamiento) en regimen …   Enciclopedia Universal

  • Bernoulli — Saltar a navegación, búsqueda Los Bernoulli (o Bernouilli) son una familia de matemáticos y físicos suizos procedentes de la ciudad de Basilea, que irrumpió en el mundo científico a finales del siglo XVII. El fundador de esta familia fue Jacob el …   Wikipedia Español

  • principio — (Del lat. principium.) ► sustantivo masculino 1 Primer instante del ser de una persona o cosa: ■ conocemos el principio de nuestra vida, pero no el fin. ANTÓNIMO fin final 2 Punto considerado como primero en una cosa: ■ quedamos en el principio… …   Enciclopedia Universal

  • Bernoulli, familia — Dos generaciones de distinguidos matemáticos suizos. Jakob (n. 1655–m. 1705) y Johann (n. 1667–m. 1748) eran los hijos de un farmacéutico que quería que uno de ellos estudiara teología y el otro medicina. A pesar de sus objeciones, ambos… …   Enciclopedia Universal

  • Bernoulli, principio de — o teorema de Bernoulli Principio que relaciona entre sí la presión, la velocidad y la altura o cota para un fluido sin viscosidad con un flujo constante. Una consecuencia es que, para un flujo horizontal, a medida que la velocidad del fluido… …   Enciclopedia Universal

  • Bernoulli — Familia de matemáticos suizos que se inicia a finales del siglo XVII con Johann I y Jakob I. Destacaron en la enseñanza y desarrollo de las matemáticas, en especial Jakob I, Johann I, Daniel, Johann III y Nikolaus II. * * * Bernoulli, Daniel… …   Enciclopedia Universal

  • Daniel Bernoulli — Saltar a navegación, búsqueda Daniel Bernoulli Retrato por Johann Rudolf Huber …   Wikipedia Español

  • Iomega Bernoulli Box — Disco Bernoulli de 230 MB. El Bernoulli Box (o simplemente Bernoulli) es un dispositivo removible de almacenamiento masivo diseñado y comercializado por Iomega en 1983. Fue su primer producto popular. El desarrollo comenzó en 1980 y tomó dos años …   Wikipedia Español

  • Teorema de Bernoulli — Para el comportamiento físico de un fluido, véase Principio de Bernoulli. El Teorema de Bernoulli es un caso particular de la Ley de los grandes números, que precisa la aproximación frecuencial de un suceso a la probabilidad p de que este ocurra… …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”