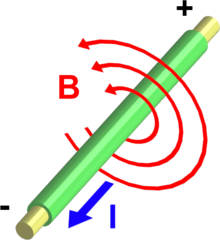
Ley de Ampère

Una corriente eléctrica produce un campo magnético, siguiendo la Ley de Ampère.

En física del magnetismo, la ley de Ampère, modelada por André-Marie Ampère en 1826,^[1] relaciona un campo magnético estático con la causa que la produce, es decir, una corriente eléctrica estacionaria. James Clerk Maxwell la corrigió posteriormente y ahora es una de las ecuaciones de Maxwell, formando parte del electromagnetismo de la física clásica.

Contenido

1 Ampliación de la ley original: Ley de Ampère-Maxwell
- 1.1 Forma integral
- 1.2 Forma diferencial
2 Ejemplos de aplicación
- 2.1 Hilo conductor infinito
3 Forma del ángulo sólido
4 Véase también
5 Referencias

Ampliación de la ley original: Ley de Ampère-Maxwell

La ley de Ampère-Maxwell o ley de Ampère generalizada es la misma ley corregida por James Clerk Maxwell que introdujo la corriente de desplazamiento, creando una versión generalizada de la ley e incorporándola a las ecuaciones de Maxwell.

Forma integral

$\oint_C \vec{H} \cdot d\vec{l} = \iint_S \vec{J} \cdot d \vec{S} + {d \over dt} \iint_S \vec{D} \cdot d \vec{S}$

siendo el último término la corriente de desplazamiento.

siempre y cuando la corriente sea constante y directamente proporcional al campo magnético, y su integral (E) por su masa relativa.

Forma diferencial

Esta ley también se puede expresar de forma diferencial, para el vacío:

$\vec\nabla\times\vec B = \mu_0 \vec J + \mu_0 \epsilon_0 \frac{\partial\vec E}{\partial t}$

o para medios materiales:

$\vec\nabla\times\vec H = \vec J + \frac{\partial\vec D}{\partial t}$

Ejemplos de aplicación

Hilo conductor infinito

Campo magnético creado por un hilo conductor de longitud infinita por el que circula una corriente $I_0\,$ , en el vacío.

El objetivo es determinar el valor de los campos $\vec{H}$ , $\vec{B}$ y $\vec{M}$ en todo el espacio.

Escribimos la Ley de Ampère:

$\oint_C \vec{H} \cdot d\vec{l}=I_{enc}$ .

Utilizamos coordenadas cilíndricas por las características de simetría del sistema.
Definimos una curva alrededor del conductor. Es conveniente tomar una circunferencia de radio $ρ$ .
El diferencial de longitud de la curva será entonces $d\vec{l}=dl\hat{\phi}=r d\phi\hat{\phi}$
Para este caso, la corriente encerrada por la curva es la corriente del conductor: $I\,$

$\oint_{Circ} \vec{H} \cdot \rho \cdot d\phi\hat{\phi}=I_0$ .

Como el sistema posee simetría radial (Es indistinguible un punto cualquiera de la circunferencia $C\,$ de otro que esté en otro ángulo sobre la misma curva), podemos decir que el campo $\vec{H}$ y el radio $ρ$ son independientes de la coordenada $\phi\,$ . Por lo tanto pueden salir fuera de la integral. Integramos para toda la circunferencia, desde 0 a $2π$ .

$\vec{H} \cdot \rho \cdot \int_0^{2\pi} d\vec{\phi}=I_0$ .

La integral que queda no es más que el perímetro de la circunferencia: $2\pi\rho\,$ .
Despejamos $\vec{H}$ y nos queda en función de $ρ$ . La dirección es en $\hat{\phi}$ , por la regla de la mano derecha:

$\vec{H}(\rho)= \frac {I_0} {2\pi\rho} \hat{\phi}$

Como estamos trabajando en el vacío, $μ = μ 0$ , por lo tanto:

$\vec{B}(\rho)= \frac {\mu_0 I_0} {2\pi\rho} \hat{\phi}$

Y por la misma razón, en ausencia de materiales magnéticos:

$\vec{M}(\rho)= 0$

Forma del ángulo sólido

Si c es un lazo cerrado por el cual circula una corriente i, y Ω es el ángulo sólido formado por el circuito y el punto en el que se calcula el campo, entonces la intensidad de campo magnético está dada por:

$\vec H = i \,\vec\nabla\, \Omega$

Véase también

Referencias

↑ Richard Fitzpatrick (2007). «Ley de Ampère».

Griffiths, David J. (1998). Introduction to Electrodynamics (3ª ed.). Prentice Hall. ISBN 0-13-805326-X.
Tipler, Paul (2004). Physics for Scientists and Engineers: Electricity, Magnetism, Light, and Elementary Modern Physics (5ª ed.). W. H. Freeman. ISBN 0-7167-0810-8.
Tipler, Paul (2005). "Física para la ciencia y la tecnología). 5 edición. (Editorial Reverte)

Categorías:

Leyes electromagnéticas
Leyes epónimas

Wikimedia foundation. 2010.

Игры ⚽ Поможем решить контрольную работу

Mira otros diccionarios:

Ley de Ampère — En física, la ley de Ampère es la equivalente magnética de la ley de Gauss, descubierta por André Marie Ampère. Explica que la circuilación de la intensidad del campo magnético en un contorno cerrado es igual a la corriente que lo recorre en ese… … Enciclopedia Universal
Ley (desambiguación) — Ley puede referirse a: Contenido 1 Derecho 2 Ciencias 3 Metafísica 4 Libros 5 Música … Wikipedia Español
Ley de Gauss — Para el Teorema de Gauss, véase Teorema de la divergencia. En física y en análisis matemático, la ley de Gauss relaciona el flujo eléctrico a través de una superficie cerrada y la carga eléctrica encerrada por esta superficie. De esta misma forma … Wikipedia Español
Ley de Faraday — Este artículo o sección necesita referencias que aparezcan en una publicación acreditada, como revistas especializadas, monografías, prensa diaria o páginas de Internet fidedignas. Puedes añadirlas así o avisar … Wikipedia Español
Ampère, André Marie — (22 ene. 1775, Lyon, Francia–10 jun. 1836, Marsella). Físico francés, fundador de la ciencia del electromagnetismo. Niño prodigio, a los 12 años de edad ya dominaba todo el campo conocido de la matemática. Fue profesor de física, química y… … Enciclopedia Universal
Ampère, ley de — Ley del electromagnetismo que describe matemáticamente la fuerza magnética entre dos corrientes eléctricas. Lleva el nombre de André Marie Ampère, quien descubrió la existencia de estas fuerzas. Si dos corrientes fluyen en la misma dirección, la… … Enciclopedia Universal
Ley — I (Del lat. lex, legis.) ► sustantivo femenino 1 FÍSICA Regla natural, constante e invariable a la que están sometidos los fenómenos de la naturaleza: ■ la ley de la gravitación universal fue enunciada por Newton. 2 Disposición dictada por una… … Enciclopedia Universal
Maxwell Ampère — Maxwell Ampère, ley de … Enciclopedia Universal
Maxwell Ampère, ley de — ► ELECTROMAGNETISMO Caso particular de las ecuaciones de Maxwell que da el valor del rotacional del campo magnético, cuando el campo eléctrico no depende explícitamente del tiempo … Enciclopedia Universal
Ecuaciones de Maxwell — Las cuatro ecuaciones de Maxwell describen todos los fenómenos electromagnéticos, aquí se muestra la inducción magnética por medio de una co … Wikipedia Español

Los diccionarios y las enciclopedias sobre el Académico

Ley de Ampère

Contenido