Electromagnetismo

Electromagnetismo
Ferrofluido que se agrupa cerca de los polos de un magneto poderoso.

El electromagnetismo es una rama de la física que estudia y unifica los fenómenos eléctricos y magnéticos en una sola teoría, cuyos fundamentos fueron sentados por Michael Faraday y formulados por primera vez de modo completo por James Clerk Maxwell. La formulación consiste en cuatro ecuaciones diferenciales vectoriales que relacionan el campo eléctrico, el campo magnético y sus respectivas fuentes materiales (corriente eléctrica, polarización eléctrica y polarización magnética), conocidas como ecuaciones de Maxwell.

El electromagnetismo es una teoría de campos; es decir, las explicaciones y predicciones que provee se basan en magnitudes físicas vectoriales o tensoriales dependientes de la posición en el espacio y del tiempo. El electromagnetismo describe los fenómenos físicos macroscópicos en los cuales intervienen cargas eléctricas en reposo y en movimiento, usando para ello campos eléctricos y magnéticos y sus efectos sobre las sustancias sólidas, líquidas y gaseosas. Por ser una teoría macroscópica, es decir, aplicable sólo a un número muy grande de partículas y a distancias grandes respecto de las dimensiones de éstas, el electromagnetismo no describe los fenómenos atómicos y moleculares, para los que es necesario usar la mecánica cuántica.

El electromagnetismo considerado como fuerza es una de las cuatro fuerzas fundamentales del universo actualmente conocido.

Contenido

Historia

Artículo principal: Historia del electromagnetismo

Desde la antigua Grecia se conocían los fenómenos magnéticos y eléctricos pero no es hasta inicios del siglo XVII donde se comienza a realizar experimentos y a llegar a conclusiones científicas de estos fenómenos.[1] Durante estos dos siglos, XVII y XVIII, grandes hombres de ciencia como William Gilbert, Otto von Guericke, Stephen Gray, Benjamin Franklin, Alessandro Volta entre otros estuvieron investigando estos dos fenómenos de manera separada y llegando a conclusiones coherentes con sus experimentos.

Michael Faraday.

A principios del siglo XIX Hans Christian Ørsted encontró evidencia empírica de que los fenómenos magnéticos y eléctricos estaban relacionados. De ahí es que los trabajos de físicos como André-Marie Ampère, William Sturgeon, Joseph Henry, Georg Simon Ohm, Michael Faraday en ese siglo, son unificados por James Clerk Maxwell en 1861 con un conjunto de ecuaciones que describían ambos fenómenos como uno solo, como un fenómeno electromagnético.[1]

James Clerk Maxwell.

Las ahora llamadas ecuaciones de Maxwell demostraban que los campos eléctricos y los campos magnéticos eran manifestaciones de un solo campo electromagnético. Además describía la naturaleza ondulatoria de la luz, mostrándola como una onda electromagnética.[2] Con una sola teoría consistente que describía estos dos fenómenos antes separados, los físicos pudieron realizar varios experimentos prodigiosos e inventos muy útiles como la bombilla eléctrica por Thomas Alva Edison o el generador de corriente alterna por Nikola Tesla.[3] El éxito predicitivo de la teoría de Maxwell y la búsqueda de una interpretación coherente de sus implicaciones, fue lo que llevó a Albert Einstein a formular su teoría de la relatividad que se apoyaba en algunos resultados previos de Hendrik Antoon Lorentz y Henri Poincaré.

En la primera mitad del siglo XX, con el advenimiento de la mecánica cuántica, el electromagnetismo tenía que mejorar su formulación con el objetivo de que fuera coherente con la nueva teoría. Esto se logró en la década de 1940 cuando se completó una teoría cuántica electromagnética o mejor conocida como electrodinámica cuántica.

Electrostática

Artículo principal: Electrostática
Un electroscopio usado para medir la carga eléctrica de un objeto.

Cuando hablamos de electrostática nos referimos a los fenómenos que ocurren debido a una propiedad intrínseca y discreta de la materia, la carga, cuando es estacionaria o no depende del tiempo. La unidad de carga elemental, es decir, la más pequeña observable, es la carga que tiene el electrón.[4] Se dice que un cuerpo está cargado eléctricamente cuando tiene exceso o falta de electrones en los átomos que lo componen. Por definición el defecto de electrones se la denomina carga positiva y al exceso carga negativa.[5] La relación entre los dos tipos de carga es de atracción cuando son diferentes y de repulsión cuando son iguales.

La carga elemental es una unidad muy pequeña para cálculos prácticos, es por eso que en el sistema internacional a la unidad de carga eléctrica, el culombio, se le define como la cantidad de carga de 6,25 x 1018 electrones.[4] El movimiento de electrones por un conductor se denomina corriente eléctrica y la cantidad de carga eléctrica que pasa por unidad de tiempo se la define como intensidad de corriente. Se pueden introducir más conceptos como el de diferencia de potencial o el de resistencia, que nos conduciría ineludiblemente al área de circuitos eléctricos, y todo eso se puede ver con más detalle en el artículo principal.

El nombre de la unidad de carga se debe a Coulomb quien en 1785 llegó a una relación matemática de la fuerza eléctrica entre cargas puntuales, que ahora se la conoce como ley de Coulomb:

\vec{F} = \frac{1}{4 \pi \varepsilon_0} \frac{q_1 q_2}{r^2} \vec{e_r}

Entre dos cargas puntuales \ q_1 y \ q_2 existe una fuerza de atracción o repulsión \vec F que varía de acuerdo al cuadrado de la distancia \ r^2 entre ellas y de dirección radial \vec {e_r}; y ε0 es una constante conocida como permitividad eléctrica.

Las cargas elementales al no encontrarse solas se las debe tratar como una distribución de ellas. Es por eso que debe implementarse el concepto de campo, definido como una región del espacio donde existe una magnitud escalar o vectorial dependiente o independiente del tiempo. Así el campo eléctrico \vec E está definido como la región del espacio donde actúan las fuerzas eléctricas. Su intensidad se define como el límite al que tiende la fuerza de una distribución de carga sobre una carga positiva que tiende a cero, así: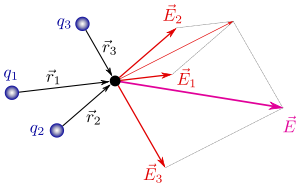

Campo eléctrico de cargas puntuales.
\vec E = \lim_{\Delta q \to 0} \frac{\vec F_{\Delta q}}{\Delta q}

Y así finalmente llegamos a la expresión matemática que define el campo eléctrico:

\vec E= \frac{q}{4\pi\varepsilon_0 r^2}\vec{e_r}

Es importante conocer el alcance de este concepto de campo eléctrico, éste nos brinda la oportunidad de conocer cuál es su intensidad y qué ocurre con una carga en cualquier parte de dicho campo sin importar el desconocimiento de qué lo provoca.[6]

Una forma de obtener qué cantidad de fuerza eléctrica pasa por cierto punto o superficie del campo eléctrico es que se ideó el concepto de flujo eléctrico. Este flujo eléctrico Φ se define como la suma de la cantidad de campo que atraviesa un área determinada, así:

\Phi = \sum \vec E \cdot \Delta \vec S = \oint_s \vec E \cdot d\vec S

El matemático y físico, Carl Friedrich Gauss, demostró que la cantidad de flujo eléctrico en un campo es igual al cociente de la carga encerrada por la superficie en la que se calcula el flujo, \ q_{enc}, y la permitividad eléctrica,ε0. Esta relación se conoce como ley de Gauss:

(1) \Phi = \oint_s \vec E \cdot d\vec S = \frac{q_{enc}}{\varepsilon_0}

Véanse también: Carga eléctrica, Ley de Coulomb, Campo eléctrico, Potencial eléctrico y Ley de Gauss

Magnetostática

Artículo principal: Magnetostática
Líneas de fuerza de una barra magnética.

No fue sino hasta el año de 1820, cuando Hans Christian Ørsted descubrió que el fenómeno magnético estaba ligado al eléctrico, que se obtuvo una teoría científica para el magnetismo.[7] La presencia de una corriente eléctrica, o sea, de un flujo de carga debido a una diferencia de potencial, genera una fuerza magnética que no varía en el tiempo. Si tenemos una carga a una velocidad \ \vec v, ésta generará un campo magnético \ \vec B que es perpendicular a la fuerza magnética inducida por el movimiento en esta corriente, así:

\vec F = q \vec v \times \vec B

Para determinar el valor de ese campo magnético, Jean Baptiste Biot en 1820,[8] dedujo una relación para corrientes estacionarias, ahora conocida como ley de Biot-Savart:

\vec B = \frac{\mu_0 I}{4 \pi} \oint_c {\frac{d\vec l \times \vec r}{r^3}}

Donde \mu_0\, es un coeficiente de proporcionalidad conocido como permeabilidad magnética, I\, es la intensidad de corriente, el d\vec l es el diferencial de longitud de la corriente y \vec r es la dirección de la corriente. De manera más estricta, \vec B es la inducción magnética, dicho en otras palabras, es el flujo magnético por unidad de área. Experimentalmente se llegó a la conclusión que las líneas de fuerza de campos magnéticos eran cerradas, eliminando la posibilidad de un monopolo magnético. La relación matemática se la conoce como ley de Gauss para el campo magnético:

(2) \oint_S \vec B \cdot d\vec S = 0

Además en la magnetostática existe una ley comparable a la de Gauss en la electrostática, la ley de Ampère. Ésta ley nos dice que la circulación en un campo magnético es igual a la densidad de corriente que exista en una superficie cerrada:

\oint_c \vec B \cdot d\vec l = \mu_0 I

Cabe indicar que esta ley de Gauss es una generalización de la ley de Biot-Savart. Además que las fórmulas expresadas aquí son para cargas en el vacío, para más información consúltese los artículos principales.

Véanse también: Ley de Ampère, Corriente eléctrica, Campo magnético, Ley de Biot-Savart y Momento magnético dipolar

Electrodinámica clásica

Artículo principal: Electrodinámica

Hasta el momento se han estudiado los campos eléctricos y magnéticos que no varían con el tiempo. Pero los físicos a finales del siglo XIX descubrieron que ambos campos estaban ligados y así un campo eléctrico en movimiento, una corriente eléctrica que varíe, genera un campo magnético y un campo magnético de por si implica la presencia de un campo eléctrico. Entonces, lo primero que debemos definir es la fuerza que tendría una partícula cargada que se mueva en un campo magnético y así llegamos a la unión de las dos fuerzas anteriores, lo que hoy conocemos como la fuerza de Lorentz:

(3) \vec F = q(\vec E + \vec v \times \vec B)

Entre 1890 y 1900 Liénard y Wiechert calcularon el campo electromagnético asociado a cargas en movimiento arbitrario, resultado que se conoce hoy como potenciales de Liénard-Wiechert.

Por otro lado, para generar una corriente eléctrica en un circuito cerrado debe existir una diferencia de potencial entre dos puntos del circuito, a ésta diferencia de potencial se la conoce como fuerza electromotriz o fem. Ésta fuerza electromotriz es proporcional a la rapidez con que el flujo magnético varía en el tiempo, esta ley fue encontrada por Michael Faraday y es la interpretación de la inducción electromagnética, así un campo magnético que varía en el tiempo induce a un campo eléctrico, a una fuerza electromotriz. Matemáticamente se representada como:

(4) \oint_C \vec{E} \cdot d\vec{l} = - \frac{d}{dt}\int_S \vec B \cdot d\vec S

En un trabajo del físico James Clerk Maxwell de 1861 reunió las tres ecuaciones anteriormente citadas (1), (2) y (4) e introdujo el concepto de una corriente de desplazamiento como una densidad de corriente efectiva y llegó a la última de las ecuaciones, la ley de Ampère generalizada (5), ahora conocidas como ecuaciones de Maxwell:

(5) \oint_C \vec{B} \cdot d\vec{l} = \mu_0 \int_S \vec{j} \cdot d\vec{S} + \mu_0 \epsilon_0 \frac{d}{dt} \int_S \vec{E} \cdot d\vec{S}

Las cuatro ecuaciones, tanto en su forma diferencial como en la integral aquí descritas, fueron las revisiones hechas por Oliver Heaviside. Pero el verdadero poder de éstas ecuaciones, más la fuerza de Lorentz (3), se centra en que juntas son capaces de describir cualquier fenómeno electromagnético, además de las consecuencias físicas que posteriormente se describirán.[9]

Esquema de una onda electromagnética.

La genialidad del trabajo de Maxwell es que sus ecuaciones describen un campo eléctrico que va ligado inequívocamente a un campo magnético perpendicular a éste y a la dirección de su propagación, éste campo es ahora llamado campo electromagnético.[10] Además la solución de éstas ecuaciones permitía la existencia de una onda que se propagaba a la velocidad de la luz, con lo que además de unificar los fenómenos eléctricos y magnéticos la teoría formulada por Maxwell predecía con absoluta certeza los fenómenos ópticos.

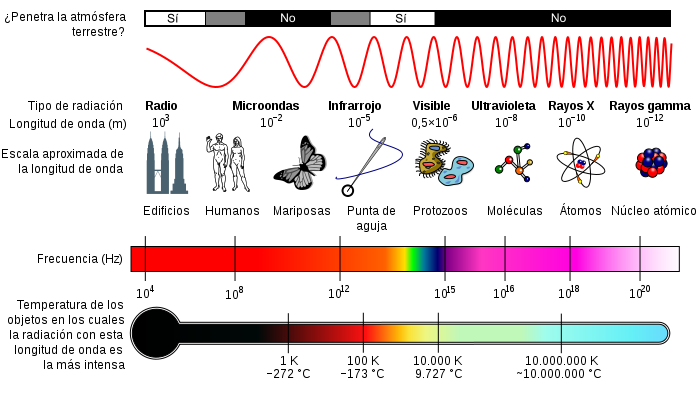
Así la teoría predecía a una onda que, contraria a las ideas de la época, no necesitaba un medio de propagación; la onda electromagnética se podía propagar en el vacío debido a la generación mutua de los campos magnéticos y eléctricos. Esta onda a pesar de tener una velocidad constante, la velocidad de la luz c, puede tener diferente longitud de onda y consecuentemente dicha onda transporta energía. La radiación electromagnética recibe diferentes nombres al variar su longitud de onda, como rayos gamma, rayos X, espectro visible, etc.; pero en su conjunto recibe el nombre de espectro electromagnético.

Espectro electromagnético.
Véanse también: Fuerza de Lorentz, Fuerza electromotriz, Ley de Ampère, Ecuaciones de Maxwell, Campo electromagnético, Radiación electromagnética y Espectro electromagnético

Formulación covariante

Artículo principal: Tensor de campo electromagnético

Clásicamente, al fijar un sistema de referencia, se puede descomponer los campos eléctricos y magnéticos del campo electromagnético. Pero al tener a un observador con movimiento relativo respecto al sistema de referencia, éste medirá efectos eléctricos y magnéticos diferentes de un mismo fenómeno electromagnético. El campo eléctrico y la inducción magnética a pesar de ser elementos vectoriales no se comportan como magnitudes físicas vectoriales, por el contrario la unión de ambos constituye otro ente físico llamado tensor y en este caso el tensor de campo electromagnético.[11]

Así, la expresión para el campo electromagnético es:

\mathbf{F} = F_{\mu \nu} = \begin{pmatrix} 0 & E_x/c & E_y/c & E_z/c \\ -E_x/c & 0 & -B_z & B_y \\ -E_y/c & B_z & 0 & -B_x \\ -E_z/c & -B_y & B_x & 0 \end{pmatrix}

Y las expresiones covariantes para las ecuaciones de Maxwell (7) y la fuerza de Lorentz (6) se reducen a:

(6) \ f_{\alpha} = \sum_{\beta} e \ F_{\alpha \beta} \ u^{\beta} \,

(7) \ \partial_{\mu} F^{\mu \nu} = \mu_0 J^{\nu} \partial_\mu \cdot F^{\mu \nu} = 0

Electrodinámica cuántica

Diagrama de Feynman mostrando la fuerza electromagnética entre dos electrones por medio del intercambio de un fotón virtual.
Artículo principal: Electrodinámica cuántica

Posteriormente a la revolución cuántica de inicios del siglo XX, los físicos se vieron forzados a buscar una teoría cuántica de la interacción electromagnética. El trabajo de Einstein con el efecto fotoeléctrico y la posterior formulación de la mecánica cuántica sugerían que la interacción electromagnética se producía mediante el intercambio de partículas elementales llamadas fotones. La nueva formulación cuántica lograda en la década de los años 40 del siglo XX describía la interacción de este fotón portador de fuerza y las otras partículas portadoras de materia.[12]

La electrodinámica cuántica es principalmente una teoría cuántica de campos renormalizada. Su desarrollo fue obra de Sinitiro Tomonaga, Julian Schwinger, Richard Feynman y Freeman Dyson alrededor de los años 1947 a 1949.[13] En la electrodinámica cuántica, la interacción entre partículas viene descrita por un lagrangiano que posee simetría local, concretamente simetría de gauge. Para la electrodinámica cuántica, el campo de gauge donde las partículas interactúan es el campo electromagnético y esas partículas son los fotones.[13]

Matemáticamente, el lagrangiano para la interacción entre fermiones mediante intercambio de fotones viene dado por:

\mathcal{L}=\bar\psi(i\gamma^\mu D_\mu-m)\psi -\frac{1}{4}F_{\mu\nu}F^{\mu\nu}. \,

Donde el significado de los términos es:

\gamma_\mu \,\! son las matrices de Dirac;
\ \psi y \bar\psi son los campos o espinores de Dirac que representan las partículas cargadas eléctricamente;
D_\mu = \partial_\mu+ieA_\mu \,\! es la derivada covariante asociada a la simetría gauge;
\ A_\mu el operador asociado al potencial vector covariante del campo electromagnético y
F_{\mu\nu} = \partial_\mu A_\nu - \partial_\nu A_\mu \,\! el operador de campo asociado tensor de campo electromagnético.
Véanse también: Teoría cuántica de campos, Ecuación de Dirac y Modelo estándar

Véase también

Referencias

  1. ↑ a b Rafael Lopez Valverde. «Historia del Electromagnetismo». Consultado el 13/02/2008.
  2. ↑ Clerk Maxwell, James (1873). «A Treatise on Electricity and Magnetism» (en inglés). Consultado el 20 de noviembre de 2007.
  3. ↑ Tesla, Nikola (1856–1943). «Obras de Nikola Tesla en Wikisource en inglés» (en inglés). Consultado el 20 de noviembre de 2007.
  4. ↑ a b J Villaruso Gato. «Cuestiones:La carga elemental». Consultado el 13/02/2008.
  5. ↑ Ministerio de Educación y Ciencia de España. «Introducción a la Electricidad». Consultado el 13/02/2008.
  6. ↑ Agustín Borrego Colomer. «Campo eléctrico». Consultado el 14/02/2008.
  7. ↑ «Introducción al electromagnetismo». Consultado el 15/02/2008.
  8. ↑ «Ley de Biot-Savart». Consultado el 15/02/2008.
  9. ↑ David Stern (2004). «Ondas electromagnéticas». Consultado el 17/02/2008.
  10. ↑ Carlos Fenandez. «La naturaleza de la luz». Consultado el 17/02/2008.
  11. ↑ Landau & Lifshitz. Teoría clásica de los campos. Ed. Reverté. ISBN 84-291-4082-4. 
  12. ↑ Enciclopedia Encarta (2007). «Electrodinámica cuántica». Consultado el 19/02/2008.
  13. ↑ a b José Antonio Montiel Tosso (Universidad de Córdoba). «Introducción a la Física cuántica. Electrodinámica cuántica». Consultado el 19/02/2008.

Bibliografía

  • Marcelo Alonso, Edward J. Finn (1976). Física. Fondo Educativo Interamericano. ISBN 84-03-20234-2. 
  • Richard Feynman (1974) (en inglés). Feynman lectures on Physics Volume 2. Addison Wesley Longman. ISBN 0-201-02115-3. 

Enlaces externos

Wikilibros


Wikimedia foundation. 2010.

Игры ⚽ Нужен реферат?

Mira otros diccionarios:

  • electromagnetismo — |èt| s. m. Ciência que trata das relações existentes entre a eletricidade e o magnetismo.   ♦ [Portugal] Grafia de eletromagnetismo antes do Acordo Ortográfico de 1990.   ♦ Grafia no Brasil: eletromagnetismo …   Dicionário da Língua Portuguesa

  • electromagnetismo — sustantivo masculino 1. (no contable) Área: física Parte de la Física que estudia las interacciones entre las corrientes eléctricas y los campos magnéticos …   Diccionario Salamanca de la Lengua Española

  • electromagnetismo — (De electro y magnetismo). m. Parte de la física que estudia la interacción de los campos eléctricos y magnéticos …   Diccionario de la lengua española

  • Electromagnetismo — ► sustantivo masculino 1 FÍSICA Magnetismo causado por una corriente eléctrica. 2 FÍSICA Ciencia que estudia las relaciones entre el magnetismo y la electricidad. * * * electromagnetismo 1 m. Fís. Conjunto de fenómenos magnéticos que se originan… …   Enciclopedia Universal

  • electromagnetismo — {{＃}}{{LM E14354}}{{〓}} {{［}}electromagnetismo{{］}} ‹e·lec·tro·mag·ne·tis·mo› {{《}}▍ s.m.{{》}} Parte de la física que estudia la interacción de los campos eléctricos y magnéticos: • El físico Ampère fue un estudioso del electromagnetismo.{{○}}… …   Diccionario de uso del español actual con sinónimos y antónimos

  • Historia del electromagnetismo — La Historia del electromagnetismo, que es el conocimiento y el uso registrado de las fuerzas electromagnéticas, data de hace más de dos mil años. En la antigüedad ya estaban familiarizados con los efectos de la electricidad atmosférica, en… …   Wikipedia Español

  • Laboratorio de Micro-ondas y electromagnetismo — EL Laboratorio de Microondas y electromagnetismo o LAME, es un instituto de investigación afiliado a el ENSEEIHT. Los temas de investigación del laboratorio son: la modelización electromagnética, dispositivos microondas y antenas, métodos… …   Wikipedia Español

  • EMC (electromagnetismo) — Saltar a navegación, búsqueda EMC corresponde en inglés a Electromagnetic Compatibility. En castellano se llama compatibilidad electromagnética (CE). Es una rama de la Ingeniería eléctrica que estudia la generación, propagación y recepción… …   Wikipedia Español

  • Biot y Savart, ley de — ► ELECTROMAGNETISMO Ley formulada por J.B. Biot y F. Savart, según la cual una corriente de intensidad I que circula por un conductor rectilíneo crea a su alrededor un campo magnético directamente proporcional a I e inversamente proporcional a la …   Enciclopedia Universal

  • Curie, ley de — ► ELECTROMAGNETISMO Ley descubierta por el matrimonio Curie según la cual en las sustancias paramagnéticas, la relación entre la intensidad de magnetización y la temperatura absoluta es inversamente proporcional …   Enciclopedia Universal

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”