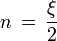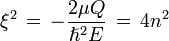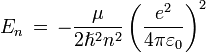- El Átomo de Hidrógeno
-
El Átomo de Hidrógeno
Contenido
El Átomo de Hidrógeno
En éste artículo se mostrará la solución cuántica al átomo de hidrógeno, este es el átomo más simple y el único sistema cuántico real que tiene solución analítica exacta. Históricamente se ha enseñado ésta solución porque además de corroborar los datos experimentales con el modelo teórico cuántico de los átomos, proporciona las herramientas fundamentales de la teoría atómica actual, y provee una solución aproximada pero muy buena para los átomos más complicados.
Descripción del átomo
El átomo de hidrógeno, es conocido también como átomo monoelectrónico, debido a que está formado por un protón que se encuentra en el núcleo del átomo y que contiene casi toda la masa del átomo, y un solo elecetrón que orbíta alrededor de dicho núcleo. En mecánica clásica, el problema equivalente es el problema de dos cuerpos, en dicho problema es conveniente hacer la descripción del sistema, colocando el origen del sistema de referencia en el centro de masa de la partícula de mayor masa, esta descripción es correcta considerando como masa de la otra partícula la masa reducida que viene dada por
el problema ahora se reduce a un problema de una sola partícula, la ecuación de Schroedinger para una partícula en tres dimensiones, independiente del tiempo viene como
notese que por la simetría esférica del potencial de coulomb responsable de la interacción entre el protón y el electrón, debemos usar coordenadas esféricas, ésto lo haremos con detalle en la siguiente sección.
La Función de Onda
En la sección anterior vimos que la ecuación de onda independiente del tiempo de una partícula sometida a un potencial
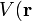 ) en tres dimensiones es
) en tres dimensiones esdonde E es la energía total de la partícula electrón, en éste caso, recordemos la simetría esférica que se puede tratar con más facilidad en coordenadas esféricas, entonces el laplaciano en coordenadas esféricas, se escribe
la justificación para utilizar éste laplaciano, aunque obviamente tiene una estructura más complicada que su igual de las coordenadas cartesianas, es que es la forma más práctica de realizar la separación de variables, ésto tambien es posible utilizando otro sistema de coordenadas, si el lector desea ver como se realiza le recomiendo L. Schiff Quantum Mechanics. Ahora nuestra ecuación queda escrita
esta es una ecuación en derivadas parciales usando la técnica de separción la convertimos en tres ecuaciones diferenciales ordinarias, pero se suele separar primero la parte radial de la angular, y eso quiere decir que la solución se reescribe como
de modo que la ecuación queda
reordenando términos se puede escribir
notese que la parte izquierda de ésta ecuación no depende de las variables de la parte derecha y viceversa, esto quiere decir que la única forma de satisfacer la igualdad es que ambas partes sean igual a una constante, para que la solución sea físicamente aceptable, la constante de separación debe ser l(l + 1) de modo que se obtienen dos ecuaciones.
Ecuación Angular
La primera es conocida en física como los Armónicos esféricos y es
y en efecto es la ecuación de Laplace en coordenadas esféricas, la solución a esta ecuación es
con
y los
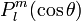 los polinomios asociados de Legendre. Estos polinomios son finitos en 0 y π como lo requiere la función de onda aceptable, la forma de construir los polinomios es entre otras, mediane la fórmula de Rodrigues que para estos polinomios es
los polinomios asociados de Legendre. Estos polinomios son finitos en 0 y π como lo requiere la función de onda aceptable, la forma de construir los polinomios es entre otras, mediane la fórmula de Rodrigues que para estos polinomios esevaluando después la en x = cosθ, la razón por la que la constante de separación se eligió como l(l + 1) fue justamente para que la solución fueran estos polinomios, dado que además de ser una solución conocida a la ecuación, es físicamente aceptable, la otra constante m aparece al aplicar el método de separación a la ecuación de los armónicos esféricos, si usted es lo suficientemene curioso y eso espero, también notará que la ecuación para
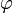 proporciona lógicamente, dos soluciones linealmente independientes, sin embargo la otra se descarta porque la densidad de probabilidad debe ser independiente de la coordenada
proporciona lógicamente, dos soluciones linealmente independientes, sin embargo la otra se descarta porque la densidad de probabilidad debe ser independiente de la coordenada 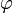 ya que no debe existir una dirección preferencial para encontrsr a electrón en el espacio, porque el espacio es isotrópico, la constante m además, solo puede ser un entero, y esto se debe a que
ya que no debe existir una dirección preferencial para encontrsr a electrón en el espacio, porque el espacio es isotrópico, la constante m además, solo puede ser un entero, y esto se debe a que 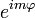 no sería monovaluada en caso contrario, por otro lado l también debe ser un entero, y positivo, para que la solución a la ecuación resultante para θ luego de la separación de variables sea aceptable, la fórmula de rodrigues se puede además estabelcer una relación entre las constantes, puesto que si | m | > l el polinomio correspondiente a las constantes dadas se anula y por consiguiente toda la función de onda, en concreto
no sería monovaluada en caso contrario, por otro lado l también debe ser un entero, y positivo, para que la solución a la ecuación resultante para θ luego de la separación de variables sea aceptable, la fórmula de rodrigues se puede además estabelcer una relación entre las constantes, puesto que si | m | > l el polinomio correspondiente a las constantes dadas se anula y por consiguiente toda la función de onda, en concretoEcuación Radial
La otra ecuación es de suma importancia, ya que su solución depende de la forma específica del potencial, de hecho para cualquier potencial esféricamente simétrico la solución anterior es válida, y la solución a ésta parte de la ecuación de onda es característica de la forma específica del potencial electrostático, en efecto la ecuación queda
donde se ha sustituido V(r) por el potencial electrostático mediante el cual interaccionan el protón y el electrón y aquí
ésta ecuación es de una dificultad consideable, pero se puede resolver si se consideran las soluciones asintóticas y luego se ajusta una solución exacta, haciendo el cambio
se tiene que la ecuación se reescribe como
si ahora se hace un cambio de variable
entonces la ecuación queda
ahora otro cambio
y ahora la ecuación es
si se considera ahora que
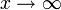 es claro que la ecuación queda
es claro que la ecuación quedala solución físicamente aceptable bajo esta condición es
luego otra consideración asintótica,
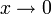 el término que depende de 1 / x2 crece mucho más rápido que los demás términos, de donde se obtiene
el término que depende de 1 / x2 crece mucho más rápido que los demás términos, de donde se obtieney la solución acpetable en éste caso es
si ahora se supone una función S(x) tal que
entonces se tendrá que satisfacer la siguiente ecuación
si ahora 2l + 1 = γ y además
con
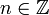 y luego β = n + l se tendría
y luego β = n + l se tendríahaciendo ahora
- 2x = ρ
se tiene finalmente
esta es la ecuación de Laguerre y su solución es
o mejor dicho
donde los
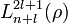 son los polinomios asociados de Laguerre y que vienen definidos por la fórmula de Rodrigues
son los polinomios asociados de Laguerre y que vienen definidos por la fórmula de Rodriguesla solución a la ecuación radial se puede entonces escribir
donde
más adelante se mostrará el valor y el significado de a0
La cuantización de la Energía "Los Niveles Del Hidrógeno"
En la solución de la parte radial de la ecuación del átomo de hidrógeno, apareció un nuevo entero positivo, de hecho mayor estrictamente que cero, y es n, en la ecuación en la que apareció se estableció
con facilidad se puede verificar que
de donde claramente
que es un resultado coincidente con la experimentación, y además por si fuera poco con el modelo del átomo de hidrógeno de Bohr
Categoría: Wikipedia:Fusionar
Wikimedia foundation. 2010.

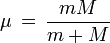
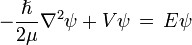
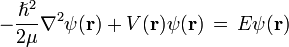
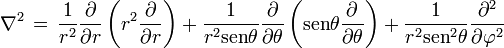
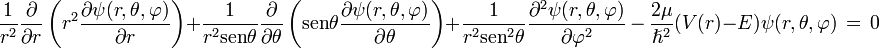
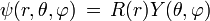
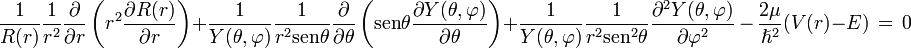
![\frac{1}{R(r)} \frac{1}{r^2} \frac{\partial }{\partial r}\left(r^2 \frac{\partial R(r)}{\partial r}\right)\, - \, \frac{2\mu }{\hslash^2}(V(r)-E) \, = \, -\frac{1}{Y(\theta, \varphi)} \left[\frac{1}{r^2 \text{sen} \theta}\frac{\partial }{\partial \theta}\left(\text{sen}\theta \frac{\partial Y(\theta, \varphi)}{\partial \theta}\right)+\frac{1}{r^2 \text{sen}^2 \theta}\frac{\partial^2 Y(\theta, \varphi)}{\partial \varphi^2} \right]](/pictures/eswiki/57/981ba76b778c6d407be4c5586e5c1d8d.png)
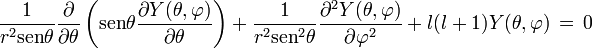
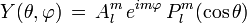
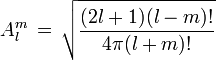
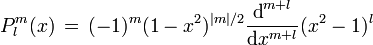
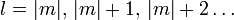
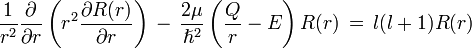
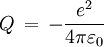
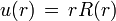
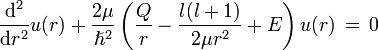

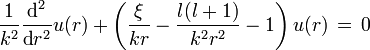
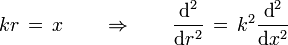
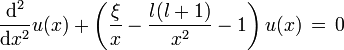
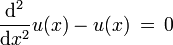
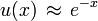
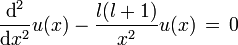
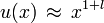
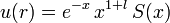
![x \frac{\text{d}^2}{\text{d}x^2}S(x)+(1-2x+(2l+1))\frac{\text{d}}{\text{d} x}S(x)+2\left(\left[\frac{\xi}{2}+l\right]-(2l+1) \right)S(x)](/pictures/eswiki/54/6c21552c848f797e19364e44f8a1681f.png)
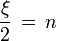
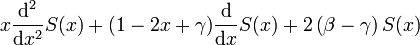
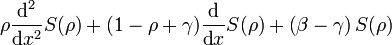
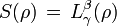
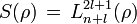
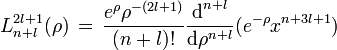
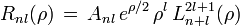
![A{nl} \, = \, \left( \frac{2}{n a_0}\right)^{3/2}\left[ \frac{(n-l-1)!}{2n [(n+l)!]^3}\right]^{1/2}](/pictures/eswiki/49/14390b13bf3b8808dcec1bced4e93f86.png)