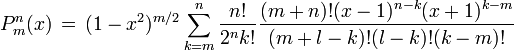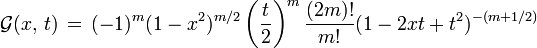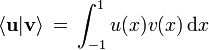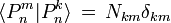- Polinomios asociados de Legendre
-
Polinomios asociados de Legendre
Los polinomios asociados de Legendre son una familia de polinomios ortogonales que tienen una aplicación muy importante en áreas como física e ingeniería, aquí se tratará de forma breve algunas de las cosas mas relevantes referentes a dichos polinomios.
Existe una ecuación diferencial, cuya solución se conoce como los polinomios asociados de Legendre; dicha ecuación aparece en la solución del átomo de hidrógeno, y otros problemas de física muy relevantes. La ecuación a la que se está haciendo referencia es
Para
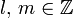 la solución a la ecuación es de la forma
la solución a la ecuación es de la formacon los
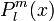 los antes mencionados polinomios asociados de Legendre, que vienen dados por la fórmula de Olinde Rodrigues
los antes mencionados polinomios asociados de Legendre, que vienen dados por la fórmula de Olinde Rodriguesen la solución del átomo de hidrógeno, y en general en la resolución de la Ecuación de Laplace en coordenadas esféricas se obtiene ésta ecuación pero escrita de otra forma, para obtenerla basta con hacer x = cosθ, la ecuación es
Contenido
Una expresión explícita
Desarrollando la fórmula de Rodrigues, se puede obtener una expresión para los polinomios, y es
ésta expresión es muy útil para realizar por ejemplo un programa que obtenga el valor de un polinomio de legendre evaluado en x = x0.
La función Generatriz y la Ortogonalidad de los Polinomios de Legendre
Existe una función con la propiedad de que si se expande en serie de Taylor alrededor de x0 = 0, los coeficientes de la expansión son los Polinomios Asociados de Legendre, dicha función es
ésta función es especialmente útil al querer hacer cálculos que por ejemplo involucren integrar los polinomios de legendre, en particular para calcular su norma, como ya se mencionó estos son polinomios ortogonales para un producto interno definido como
entonces para los polinomios de legendre tendremos
esto quiere decir que los polinomios son base de un espacio de hilbert, y la expresión anterior se denomina relación de ortogonalidad, recurdese que hemos considerado el caso cuando m y l son enteros, el hecho de ser base de un espacio de Hilbert hace a los polinomios asociados de legendre muy importantes para la mecánica cuántica. El término Nkm que aparece en la expresión anterior es la norma de los polinomios asociados de legendre, que se puede calcular igualando el producto interno de un polinomio con si mismo a uno.
Referencias
- Arfken G.B., Weber H.J., Mathematical methods for physicists, (2001) Academic Press, ISBN 0-12-059825-6 ver sección 12.5.
- A.R. Edmonds, Angular Momentum in Quantum Mechanics, (1957) Princeton University Press, ISBN 0-691-07912-9 ver capítulo 2.
- E. U. Condon and G. H. Shortley, The Theory of Atomic Spectra, (1970) Cambridge, England: The University Press. OCLC 5388084 ver capítulo 3
- F. B. Hildebrand, Advanced Calculus for Applications, (1976) Prentice Hall, ISBN 0-13-011189-9
- Belousov, S. L. (1962), Tables of normalized associated Legendre polynomials, Mathematical tables series Vol. 18, Pergamon Press, 379p.
Véase también
- Polinomios de Legendre
- Atomo de Hidrogeno
Categorías: Ecuaciones diferenciales ordinarias | Polinomios | Funciones especiales
Wikimedia foundation. 2010.

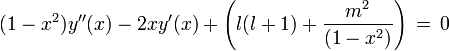
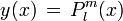
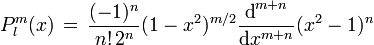
![\text{sen} \theta \frac{\text{d}}{\text{d}\theta}\left( \text{sen} \theta \frac{\text{d}}{\text{d}\theta}\Theta(\theta)\right)+\left[l(l+1)-m^2 \right]\Theta(\theta) \, = \, 0](/pictures/eswiki/54/69f5a3e67d94256e377ab8cd639f8527.png)