El problema de Apolonio consiste en hallar las circunferencias tangentes a tres circunferencias dadas. Fue propuesto (y resuelto) por Apolonio de Perga. La solución propuesta más abajo se debe a Joseph Diaz Gergonne (1771-1859).

Contenido 1 Las soluciones se presentan a pares 2 Algunas consideraciones sobre polaridad 3 Eje radical asociado a pares de soluciones 4 Solución al problema de Apolonio 5 Referencias 6 Enlaces externos

Las soluciones se presentan a pares

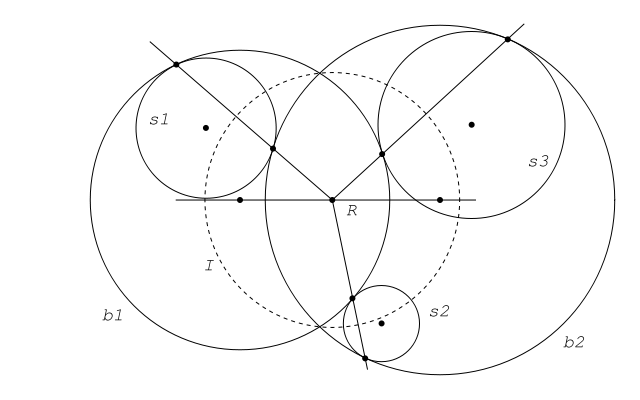
Considérense tres circunferencias (véase la figura) s1, s2 y s3. Sea R el centro radical de las circunferencias dadas. Existe una circunferencia I, ortogonal a las circunferencias dadas, cuyo centro es el punto R. En la inversión respecto de la circunferencia I, las circunferencias dadas son invariantes y las circunferencias tangentes, b1 y b2 en la figura, son homólogas.

Se sigue que los puntos de contacto entre las circunferencias buscadas y una de las circunferencias dadas, son colineales con el centro radical R. También, los centros del par de circunferencias buscadas (b1 y b2) y el centro radical, son colineales.

Algunas consideraciones sobre polaridad

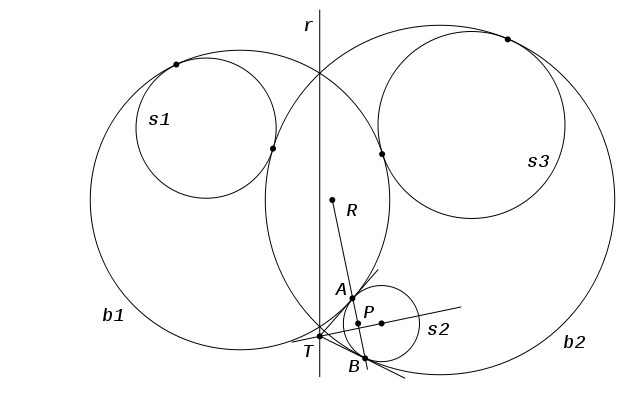
Consideremos las tangentes a las circunferencias b1 y b2 en los puntos de contacto A y B con la circunferencia s2. Si estas tangentes se cortan (como en la figura), lo hacen sobre un punto T que se halla sobre el eje radical r de las circunferencias b1 y b2. El punto T es polo de la recta AB respecto de s2 y por consiguiente, el polo P del eje radical r respecto de la misma circunferencia es colineal con los puntos de contancto A y B y con el centro radical R.

Eje radical asociado a pares de soluciones

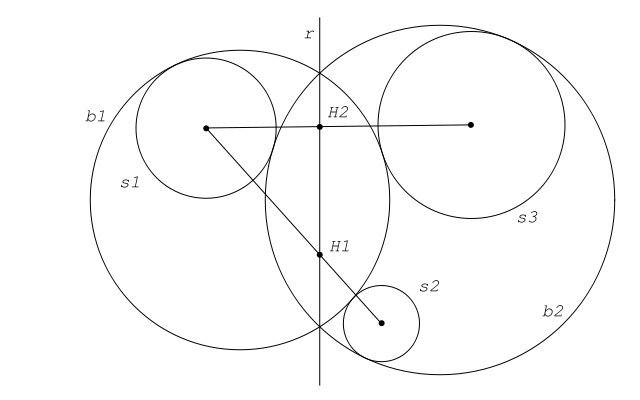
Consideremos la homotecia (de razón negativa) en la que las circunferencias s1 y s2 son homólogas, denotando con H1 el centro de dicha homotecia. H1 es centro de una inversión en la cual s1 y s2 son homólogas y las circunferencias b1 y b2 son invariantes. Por esta razón, H1 se halla sobre el eje radical del par de circunferencias b1 y b2. Otro tanto se puede decir sobre el centro de homotecia (negativa) en la cual las circunferencias s1 y s3 son homólogas. (El centro de homotecia en la cual s2 y s3 son homologas, que también se halla sobre el r, está fuera de la figura)

Se sigue que el eje radical r de las circunferencias b1 y b2 es uno de los ejes de homotecia de las circunferencias dadas.

Solución al problema de Apolonio

Las consideraciones anteriores permiten resolver el problema de Apolonio: hallar las circunferencias tangentes a tres dadas. Se puede comenzar hallando el centro radical de las tres circunferencias y se determinan los ejes de homotecia de las circunferencias. Para hallar un par de soluciones, se elige uno de estos ejes y se hallan sus polos respecto de las circunferencias dadas. Las rectas que pasan por los polos hallados y por el centro radical determinan los puntos de contacto entre las circunferencias tangentes y las circunferencias dadas.

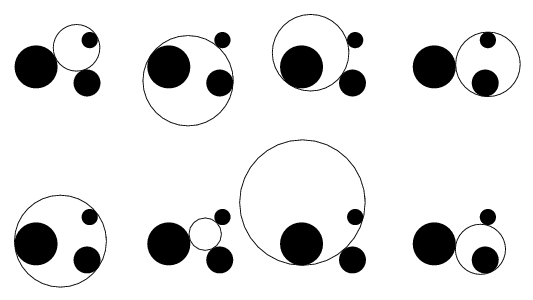
Como, en general, dadas tres circunferencias, existen cuatro ejes de homotecia, son ocho las soluciones a este problema (cuatro pares de soluciones).

Hay configuraciones de tres circunferencias que sólo admiten dos o ninguna solución.

Hay un total de ocho soluciones, las cuales están ilustradas en la siguiente gráfica:

Referencias

Jacques Hadamard, Leçons de Géométrie élémentaire, Armand Colin, Paris 1901.

Enlaces externos

Commons

• Wikimedia Commons alberga contenido multimedia sobre Problema de Apolonio.