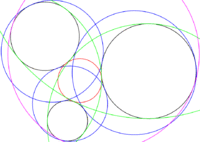- Tangencias
-
La tangencia, en geometría plana, generalmente se establece entre rectas, circunferencias, elipses, parábolas o hipérbolas, con sus distintas posiciones, tamaños y combinaciones de unas respecto de otras.
Este texto se puede considerar una ampliación gráfica de la página tangente, por tener dicha página un enfoque de carácter analítico, lejos del trabajo con regla y compás usados en delineación; por esta razón se excluyen, en los ejemplos, las ecuaciones algebraicas o numéricas.
Para un análisis más profundo y en más dimensiones, véase tangente, o superficies como cónicas o cuádricas. Hay generalizaciones más rigurosas en geometría proyectiva. Para el desarrollo de más propiedades con rectas y circunferencias véase categoría:geometría elemental.
Nomenclatura
- Recta hará referencia o indicará que las líneas rectas son indefinidas o infinitamente largas. También se usará semirrecta (si tiene un extremo) o segmento (cuando tiene dos extremos).
- Circunferencia hará referencia o indicará la cerrada totalmente. Para casos en los que no es cerrada, se usa arco de circunferencia o simplemente un arco cuando queda claro.
- Dos circunferencias, o una circunferencia y una recta, son tangentes o están en tangencia cuando tienen un único punto en común.
- Usaremos abreviaturas de colores, como N = negro (para el enunciado del problema), A = azul (pasos más representativos) y R = rojo (para la solución).
Antes de trazar la circunferencia tangente a los objetos dados, márquese levemente el lugar de tangencia, ya sea con una perpendicular a la recta tangente pasando por el centro de la circunferencia, o en otro caso uniendo con una recta los centros de dos circunferencias prolongándola hasta el supuesto lugar de tangencia. Esto ayuda a trazar arcos en los casos que se necesiten.
Tangencias simples
Serán las tangencias más frecuentes y de fácil resolución. Dependen del orden en que se dan los datos para su ejecución.
Entre una circunferencia y una recta
Objetivamente hay dos casos principales:
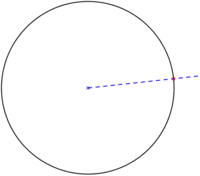
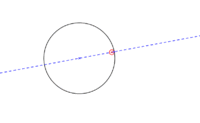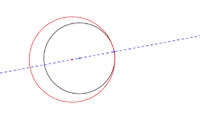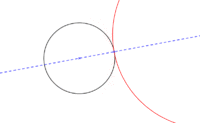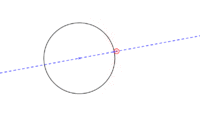
- Tenemos una circunferencia cualquiera a la que queremos trazar una recta tangente:
-
- En un primer paso se hace necesario identificar y representar el diámetro (A) de dicha circunferencia que sea perpendicular a la dirección de la recta tangente. Luego ya es cuestión de trazar la recta por los extremos (R) del diámetro hallado o radio.
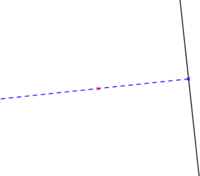
- Tenemos una recta cualquiera en la que queremos construir una circunferencia tangente:
-
- En un primer paso se hace necesaria trazar una perpendicular (A) sobre dicha recta en el punto de tangencia deseado. Luego ya es cuestión de identificar el centro de la circunferencia sobre dicha perpendicular (R) y trazar la circunferencia.
Entre dos circunferencias
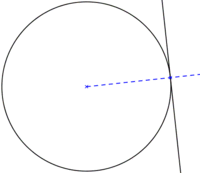
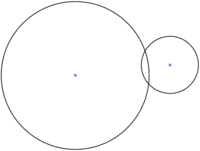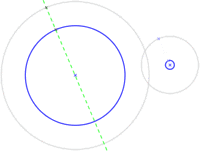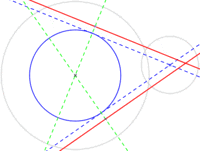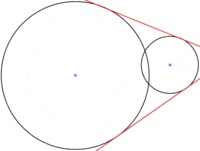
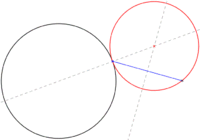
Tenemos una circunferencia (N) a la que queremos trazar otra circunferencia tangente:
- En un primer paso se hace necesario trazar una recta que pasa por el centro de la circunferencia dada y por el punto de tangencia deseado (A). Luego identificamos el centro de la segunda circunferencia (R) para acabar trazándola.
Observemos que los dos centros de las circunferencias y el lugar de tangencia de éstas siempre están alineados.
Posiciones relativas entre dos circunferencias
Los distintos adjetivos son de carácter intuitivo y ayudarán a observar, identificar y distinguir casos en los que hay o no tangencias y en qué situación se dan. Son puramente operativos e informativos, ya que en sí no resuelven ningún problema, pero facilitan su explicación para casos complejos.
Véase circunferencia para las explicaciones de algunos casos.
-
Circunferencia (R) externa o exterior a otra (N)
-
Circunferencia (R) tangente externa o exterior a otra (N)
-
Circunferencia (R) secante a otra (N)
-
Circunferencia (R) tangente interior a otra (N)
-
Circunferencia (R) interior y excéntrica a otra (N)
-
Circunferencia (R) interior y concéntrica a otra (N)
-
Circunferencia coincidente es cuando son la misma.
-
Circunferencia exterior, circundante y concéntrica.
-
Circunferencia (R) exterior, circundante y excéntrica (N)
-
Circunferencia (R) tangente, exterior y circundante a otra (N)
Algunos ejemplos de tangencias múltiples
Los casos más habituales de tangencias se resuelven usando métodos como mediatrices, bisectrices y restas longitudinales de radios, incluso métodos de homotecias o potencias, para hallar circunferencias tangentes a dos rectas y una circunferencia o también para hallar circunferencias tangentes a otras tres de distintos tamaños.
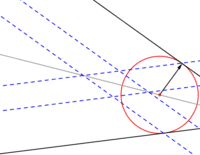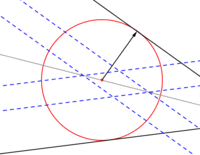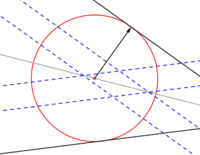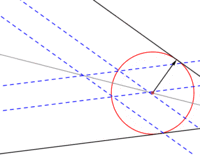
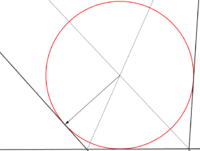
Circunferencia tangente a dos rectas dadas
- Bastará con trazar dos paralelas a las rectas dadas, equidistantes una longitud igual al radio de la circunferencia.
- El centro de la circunferencia siempre es un punto de la bisectriz del ángulo conformado por las dos rectas dadas.
Circunferencia tangente a tres rectas dadas
- Se hallarán las bisectrices de los ángulos conformados por dos parejas de rectas.
- La intersección de las dos bisectrices es el centro de la circunferencia que buscamos.
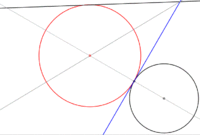
Circunferencia tangente a otra en un punto dado y a una recta dada
- Trazamos una recta tangente a la circunferencia en el punto dado.
- Trazamos la bisectriz de las dos rectas.
- Bastará con trazar una paralela a la recta dada, a una distancia igual al radio de la circunferencia pedida.
- La intersección con la bisectriz es el centro de dicha circunferencia.
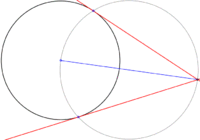
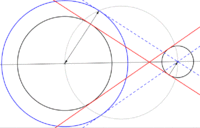
Rectas tangentes a una circunferencia dada que pasen por un punto exterior dado
- Unimos mediante un segmento el centro de la circunferencia con el punto exterior dado
- Trazamos una circunferencia auxiliar cuyo diámetro es el segmento anterior.
- La intersección de ambas circunferencias son los puntos de tangencia que al unirlos con el punto exterior nos dan la solución.
Los puntos de tangencia son los vértices del arco capaz de 90º comprendido entre el centro de la circunferencia y el punto exterior.
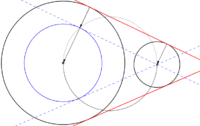
Rectas tangentes a dos circunferencias
- Podemos convertir este problema en el anterior, restando la longitud del radio de la circunferencia menor a los dos radios. Los puntos de tangencia de la circunferencia mayor estarán alineados con su centro.
- Para hallar las tangentes interiores, se suma la longitud del radio menor al mayor y se resta al menor. Los puntos de tangencia de la circunferencia mayor estarán alineados con su centro.
Circunferencia tangente a otra en un punto dado y que pase por otro punto dado
- Unimos mediante un segmento el punto tangente de las circunferencias con el punto exterior dado.
- Hallamos la mediatriz de dicho segmento.
- El centro de la circunferencia buscada estará alineado con el centro de la circunferencia dada y su punto tangente.
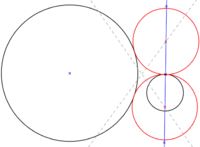
Circunferencia tangente a otra en un punto dado y a otra circunferencia cualquiera
- Es posible deducir este método del anterior.
- Alargando el radio de la circunferencia, con tangencia, y sobre su punto de tangencia, situemos dos puntos que equidisten a dicho punto el radio de la otra circunferencia. Ahora identificando mediatrices entre cada uno de los puntos y el centro de la circunferencia, que no tiene tangencia, generan otros dos puntos que son los centros de las dos circunferencias buscadas.
Circunferencias tangentes a otras tres dadas
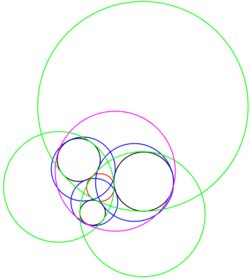
En este caso solo se menciona que aparecen varios tipos de tangencias: una tangente exterior, tres tangentes cada una exterior a una y circundante a otras dos, tres tangentes cada una exterior a dos y circundante a otra, y una tangente circundante a las tres circunferencias.
Bibliografía
- Dibujo Técnico de Jorge Senabre, Editorial Luis Vives – Zaragoza (EDELVIVES).
- Curso de dibujo geométrico y de croquización de F. Javier Rodriguez de abajo y Victor Álbarez Bengoa, Editorial MARFIL, S.A.
Categoría:- Geometría elemental
Wikimedia foundation. 2010.
