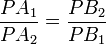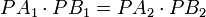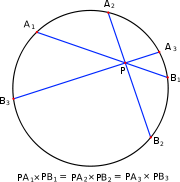
Si P es un punto que hemos fijado, y C una circunferencia, la potencia del punto P respecto a C es el producto de las distancias a cualquier par de puntos de la circunferencia alineados con P. El valor de la potencia siempre es constante para cada punto P, independientemente de la elección de los puntos de la circunferencia.

De manera más formal, si P es un punto, y una recta que pasa por P corta a la circunferencia en A y B, la potencia de P se define como el producto PA × PB, como se muestra en la figura.

El punto P puede estar localizado en cualquier parte del plano, no sólo en el interior de la circunferencia. Usualmente se consideran segmentos dirigidos,^[1] por lo que hay tres casos para el signo de la potencia:

• Si el punto P está en el interior de la circunferencia, la potencia toma valor negativo, pues PA y PB tienen sentido opuesto.
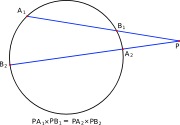
• Si el punto P está en el exterior de la circunferencia, la potencia toma valor positivo.
• Si el punto P está sobre la circunferencia, la potencia es igual a cero (pues A=P o B=P).

Contenido 1 Relación con semejanza 2 El caso de la tangente 3 Lugares geométricos 4 Construcción de la media geométrica de dos segmentos 5 Véase también 6 Referencia 6.1 Bibliografía

Relación con semejanza

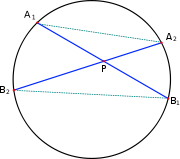
El hecho de que la potencia de un punto sea independiente de la recta está relacionado con semejanza de triángulos. Dibujando dos secantes y uniendo los puntos A y los puntos B respectivamente, obtenemos dos triángulos A₁PA₂ y B₁PB₂

Los ángulos PA₁A₂ y PB₂B₁ son iguales; ambos miden la mitad del arco B₁A₂. Como el ángulo A₁PA₂ es igual al ángulo B₁PB₂, los triángulos A₁PA₂ y B₂PB₁ son semejantes.

De la semejanza se tiene que

por lo que

El caso de la tangente

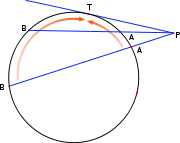
Un caso especial se obtiene cuando el punto es exterior y la recta es tangente a la circunferencia. Si PT es una tangente a la circunferencia, entonces la relación de potencia de punto se convierte en PA · PB = PT². La prueba es similar a la dada para el caso general, obteniendo aquí que los triángulos PTB y PAT son semejantes. Intuitivamente, puede entenderse la relación anterior como el caso límite en que los puntos A y B coinciden.

Lugares geométricos

Dados una circunferencia C y un número k fijo, nos podemos preguntar por todos aquellos puntos que tengan el número escogido como su potencia. En otras palabras, nos preguntamos por el lugar geométrico de los puntos cuya potencia respecto a C es igual a k.

La respuesta a la pregunta anterior se obtiene mediante la fórmula radio-distancia, que permite calcular la potencia de un punto si se conoce el radio de la circunferencia y la distancia del punto al centro.

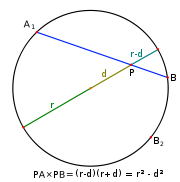
Tracemos el diámetro de la circunferencia que pasa por P. Si calculamos la potencia sobre el diámetro obtenemos (r-d)(r+d)=r²-d².

La fórmula anterior nos permite calcular la potencia conociendo el radio de la circunferencia y su distancia al centro. Como consecuencia, todos los puntos a una misma distancia del centro tienen la misma potencia, y viceversa: puntos con la misma potencia son equidistantes del centro.

Un problema similar consiste en determinar el conjunto de puntos cuyas potencias respecto a dos circunferencias fijas son iguales. En este caso, el lugar geométrico es en una recta, denominada eje radical.

Construcción de la media geométrica de dos segmentos

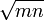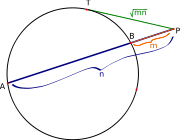
Una aplicación de la potencia de un punto, es permitir la construcción de la media geométrica de dos segmentos. Dados dos segmentos de longitudes m y n, la media geométrica es un segmento de longitud . El caso en que m=n es trivial puesto que la media geométrica es igual a ambos. Supongamos entonces que m<n.

Dibújese un segmento PA de longitud n, y dentro de él encuéntrese un punto B tal que PB tenga longitud m. Constrúyase una circunferencia con diámetro AB, la cual tiene longitud n-m. Finalmente, trácese la tangente a la circunferencia desde P. Por la propiedad de la tangente, PT²=PA·PB=m·n, por lo que PT tiene longitud 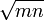. Es decir, PT es la media geométrica de PA y PB.

Véase también

• Eje radical
• El problema de Apolonio
• Demostración del teorema del coseno

Referencia

Bibliografía

• Adam, Puig (1988). Euler(Madrid) (ed.). Geometría Métrica, Tomo I, pp. 712. ISBN 84-85731-06-9.