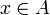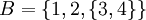- Elemento de un conjunto
-
Elemento de un conjunto
En teoría de conjuntos, un elemento o miembro de un conjunto (o familia de conjuntos) es un objeto atómico que forma parte de ese conjunto (o familia).
Contenido
Teoría de conjuntos y elementos
Al escribir A = {1,2,3,4}, estamos diciendo que los elementos del conjunto A son los números 1, 2, 3 y 4. Un grupo de elementos de A sería, por ejemplo, {1,2}, el cual es un subconjunto de A.
Los elementos pueden ser conjuntos en sí mismos. Por ejemplo, consideremos el conjunto B = {1,2,{3,4}}. Los elementos de B no son 1, 2, 3, y 4; en efecto, B tiene sólo tres elementos: 1, 2 y el conjunto {3,4}.
Los elementos de un conjunto pueden ser cualquier cosa. Por ejemplo, C = {rojo, verde, azul}, es el conjunto cuyos elementos son los colores rojo, verde y azul.
Notación
La relación "es un elemento de", también llamada miembro del conjunto, se denota mediante el símbolo
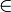., y al escribirestamos diciendo que x es un elemento de A. Equivalentemente, podemos decir o escribir "x es un miembro de A", "x pertenece a A", "x es en A", "x reside en A", "A incluye x", o "A contiene x". La negación de este símbolo se denota
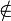.Desafortunadamente, los términos "A incluye x" y "A contiene x" son ambiguos, porque algunos autores también los usan para referirse a que "x es un subconjunto de A".[1] El lógico George Boolos es enfático al aclarar que la palabra "contiene" debe usarse sólo para pertenencia de elementos, e "incluye" sólo para relaciones de subconjuntos[2]
Cardinalidad de conjuntos
El número de elementos en un conjunto particular es una propiedad conocida como cardinalidad, que informalmente se conoce como el tamaño de un conjunto. Para los ejemplos anteriores, la cardinalidad del conjunto A es 4, mientras que la de B y C es 3. Un conjunto finito es aquel con un número finito de elementos, mientras que uno infinito, uno con una cantidad infinita de elementos. Los ejemplos de arriba son todos de conjuntos finitos. Un ejemplo de conjunto infinito es el conjunto de los números naturales,
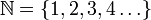.Ejemplos
Usando los conjuntos definidos arriba:
podemos decir que:
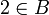
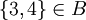
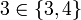
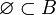
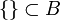
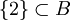
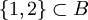
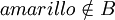
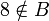
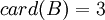
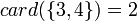
- La cardinalidad de
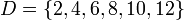es finita e igual a 6. - La cardinalidad de
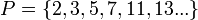(los números primos) es infinita.
Notas
- ↑ Eric Schechter (1997). Handbook of Analysis and Its Foundations. Academic Press. ISBN 0-12-622760-8. p. 12
- ↑ (4 de febrero, 1992) 24.243 Classical Set Theory (lecture)...
Referencias
- Paul R. Halmos 1960, Naive Set Theory, Springer-Verlag, NY, ISBN 0-387-90092-6. "Naive" significa que no está completamente axiomatizado, que no es tonto ni fácil.
- Patrick Suppes 1960, 1972, Axiomatic Set Theory, Dover Publications, Inc. NY, ISBN 0-486-61630-4. La noción de conjunto (una colección de elementos), miembros o elementos, los axiomas de extensión, separación y de unión o suma son necesarios para un mayor entendimiento de este concepto.
Categoría: Teoría de conjuntos
Wikimedia foundation. 2010.
