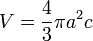- Esferoide
-
Esferoide
Esferoide oblato.
Esferoide prolato.Un esferoide es un elipsoide de revolución, es decir, la superficie que se obtiene al girar una elipse alrededor de uno de sus ejes principales c.
Por convenio, el eje de simetría se denomina c y se situa en el eje de coordenadas cartesianas z.[1]
El eje perpendicular al de simetría se llama a.
Si a > c (el eje de simetría es el menor), la superficie se llama esferoide oblato (achatado).
Si a < c (el eje de simetría es el mayor), la superficie se llama esferoide prolato (alargado).
Si a = c (el eje de simetría es igual), la superficie es una esfera.
La esfera es un caso especial de esferoide, donde la curva generatriz es una elipse de ejes iguales, es decir, una circunferencia.
Un esferoide es un caso especial de elipsoide, donde dos de los tres ejes principales son iguales.
La forma de la superficie de la Tierra se aproxima a un esferoide oblato, ligeramente achatada en los polos.
Contenido
Parametrización
La ecuación de un esferoide, en coordenadas cartesianas, centrado en el origen, es:
siendo a y c los semiejes, estando situado c en el eje de coordenadas z.
Superficie
La superficie de un esferoide puede expresarse de diversas formas:
.
-
-
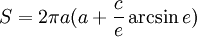- siendo e la excentricidad de la elipse:
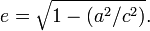
- siendo e la excentricidad de la elipse:
-
-
-
- siendo e la excentricidad de la elipse:
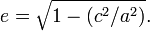
- siendo e la excentricidad de la elipse:
-
a y c son los semiejes, estando situado c en el eje de coordenadas z.
Volumen
El volumen de un esferoide es:
siendo a y c los semiejes, estando situado c en el eje de coordenadas z.
Referencias
- ↑ Eric W.: Spheroid
Enlaces externos
Categoría: Superficies
![S = \pi\left[ 2a^2 + \frac{c^2}{e} \ln\left(\frac{1+e}{1-e}\right) \right]](/pictures/eswiki/48/042118a1d2d538767b534bf01e33e778.png)
Wikimedia foundation. 2010.
