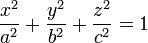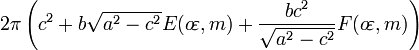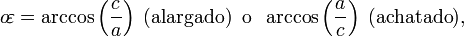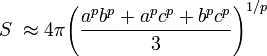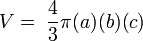Elipsoide

Elipsoide

Elipsoide

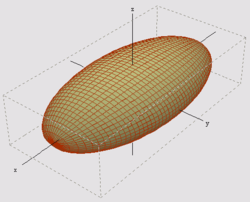
Ellipsoide.png

Un elipsoide es una superficie curva cerrada cuyas tres secciones ortogonales principales son elípticas, es decir, las originadas por planos que contienen dos ejes cartesianos.

En matemáticas, es una cuádrica análoga a la elipse, pero en tres dimensiones.

Un elipsoide se obtiene al «deformar» una esfera, mediante una transformación homológica, en la dirección de sus tres diámetros ortogonales.

Contenido

Ecuación cartesiana de un elipsoide

La ecuación general de un elipsoide con centro en el origen de coordenadas, es:

{x^2 \over a^2}+{y^2 \over b^2}+{z^2 \over c^2}=1

donde a, b y c son los semiejes del elipsoide respecto de los ejes x, y , z; son números reales positivos y determinan la forma del elipsoide. Si dos de estos semiejes son iguales, el elipsoide es un esferoide; si los tres son iguales, se trata de una esfera.

Superficie

La superficie de un elipsoide tiene la siguiente ecuación:

2\pi\left(c^2+b\sqrt{a^2-c^2}E(o\!\varepsilon,m)+\frac{bc^2}{\sqrt{a^2-c^2}}F(o\!\varepsilon,m)\right)\,\!

donde:

o\!\varepsilon=\arccos\left(\frac{c}{a}\right)\;\textrm{(alargado)\;\;o\;\;}\arccos\left(\frac{a}{c}\right)\;(\textrm{achatado}),\,\!
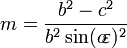m=\frac{b^2-c^2}{b^2\sin(o\!\varepsilon)^2}\,\! es la excentricidad angular,
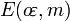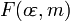E(o\!\varepsilon,m)\,\!, F(o\!\varepsilon,m)\,\! son integrales elípticas de primer y segundo orden.

Una ecuación aproximada de su superficie es:

S\;\approx 4\pi\!\left(\frac{ a^p b^p+a^p c^p+b^p c^p }{3}\right)^{1/p}\,\!

Donde p ≈ 1,6075. Con esta expresión se obtiene un error máximo de ±1,061%, en función de los valores de a, b y c

Volumen

El volumen interior de un elipsoide viene dado por la ecuación:

V=\;\frac{4}{3}\pi (a)(b)(c)\,\!

Otras características

La intersección de un elipsoide con un plano suele ser una elipse. También puede ser una circunferencia.

Se puede definir un elipsoide en espacios de más de tres dimensiones.

Véase también

Enlaces externos

Obtenido de "Elipsoide"

Wikimedia foundation. 2010.

Игры ⚽ Нужен реферат?

Mira otros diccionarios:

  • elipsóide — adj. 2 g. 1. Que tem a forma de uma elipse. • s. m. 2. Sólido produzido pela revolução da metade de uma elipse em volta de um dos seus eixos. • s. f. 3. Curva um tanto semelhante à elipse.   ♦ Grafia de elipsoide antes do Acordo Ortográfico de… …   Dicionário da Língua Portuguesa

  • elipsoide — (De elipse y oide). m. Geom. Sólido cuyas secciones planas son todas elipses o círculos. elipsoide de revolución. m. Geom. El engendrado por la rotación de una elipse alrededor de un diámetro principal …   Diccionario de la lengua española

  • elipsoide — |ói| adj. 2 g. 1. Que tem a forma de uma elipse. • s. m. 2. Sólido produzido pela revolução da metade de uma elipse em volta de um dos seus eixos. • s. f. 3. Curva um tanto semelhante à elipse …   Dicionário da Língua Portuguesa

  • elipsoide — sustantivo masculino 1. Área: geometría Cuerpo geométrico limitado en todos los sentidos, cuyas secciones planas son todas elipses o círculos …   Diccionario Salamanca de la Lengua Española

  • Elipsoide — ► sustantivo masculino 1 GEOMETRÍA Figura geométrica limitada en todos sus sentidos, cuyas secciones planas son todas elipses o círculos. FRASEOLOGÍA elipsoide de revolución GEOMETRÍA Aquel en que todas las secciones perpendiculares a uno de sus… …   Enciclopedia Universal

  • elipsoide — {{＃}}{{LM E14404}}{{〓}} {{［}}elipsoide{{］}} ‹e·lip·soi·de› {{《}}▍ s.m.{{》}} Cuerpo geométrico en tres dimensiones engendrado por el giro de una elipse en torno a su eje mayor, y cuyas secciones planas son elipses o círculos: • La superficie del… …   Diccionario de uso del español actual con sinónimos y antónimos

  • elipsoide — m Sуlido cuyas secciones planas son elipses o cнrculos …   Diccionario de Construcción y Arquitectur

  • elipsoide de revolución — ► locución GEOMETRÍA Aquel en que todas las secciones perpendiculares a uno de sus ejes son círculos …   Enciclopedia Universal

  • Geodesia — Modelo digital del terreno del Cantón del Valais. El término Geodesia, del griego γη ( tierra ) y δαιζω ( dividir ) fue usado inicialmente por Aristóteles (384 322 a. C.) y puede significar, tanto divisiones geográficas de la tierra ,… …   Wikipedia Español

  • Marea — Para otros usos de este término, véase Marea (desambiguación). Vistas a pleamar y cuando baja del puerto de La Flotte en la isla de Ré (Francia) en el golfo de Vizcaya. La marea es el cambio periódico del nivel del mar, producido principalmente… …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”