El concepto de emparejamiento aquí tratado es referente al campo de las matemáticas, específicamente al álgebra lineal. Con aplicaciones prácticas en el área de la criptografía.

Definición

Sea R un anillo comutativo más la unidad, y sean M, N y L tres R-módulos.

Un emparejamiento es cualquier mapa bilinear R 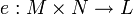. Que satisfaga:e(rm,n) = e(m,rn) = re(m,n)

para cualquier 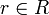. O equivalentemente, un emparejamiento es un mapa linear R: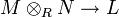

donde 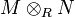denota el producto tensorial de M y N.

Un emparejamiento también puede ser considerado como un mapa linear R 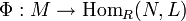, que satisfaga la primera definición y establezca Φ(m)(n): = e(m,n).

Un emparejamiento es llamado no degenerativo si para el mismo mapa se tiene que e(m,n) = 1 para todo valor de m y n = 0.

Ejemplos

Cualquier producto escalar en un espacio vectorial V real es un emparejamiento (sean M = N = V, R = R en las definiciones anteriores).

El mapa determinante (matriz 2 × 2 en k) 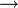k se puede considerar como un emparejamiento .

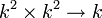El mapa de Hopf 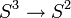definido como 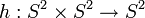es un ejemplo de un emparejamiento. En,^[1] Hardie et al. presentan una construcción explícita de este tipo de mapas utilizando conjuntos parcialmente ordenados.

Emparejamientos criptográficos

El cómputo de los emparejamientos criptográficos utiliza dos grupos, G₁ y G₂. Estos dos grupos son finitos, cícilos y aditivamente formulados en donde al menos uno de estos grupos tiene orden primo, denotado como r. El emparejamiento toma un elemento de cada uno de los dos grupos y los mapa hacia un tercero G_T, el cual es finito, cíclico, pero formulado multiplicativamente, también de order primo r. Un emparejamiento criptográfico útil satisface las siguientes propiedades:

• Bilineariedad:
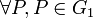  • y 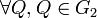, se tiene que: 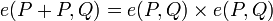y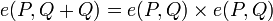
• No degeneración:
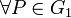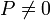  • con , existe 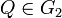tal que .
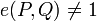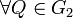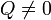  • con , existe 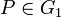tal que .
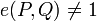• Computable:
  • e puede ser fácilmente calculado.

Los mejores métodos para calcular los emparejamientos criptográficos están basados en el algoritmo de Miller. Este método está estandarizado de facto y su mejoramiento tanto en el bucle principal como en la llamada exponenciación final es tema actual de investigación. ^{[cita requerida]}

Referencias

1. ↑ A nontrivial pairing of finite T0 spaces Authors: Hardie K.A.1; Vermeulen J.J.C.; Witbooi P.J. Fuente: Topology and its Applications, Volumen 125, Número 3, 20 de noviembre de 2002 , pp. 533-542(10)

Enlaces externos

• The Pairing-Based Crypto Lounge