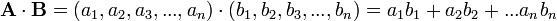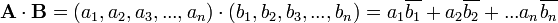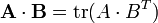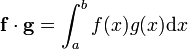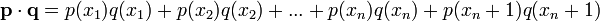Producto escalar

Saltar a navegación, búsqueda

En matemáticas el producto escalar, también conocido como producto interno, interior o punto, es una operación definida sobre un espacio vectorial cuyo resultado es una magnitud escalar.

Un espacio prehilbertiano es un espacio vectorial sobre el que se ha definido un producto escalar. Si el espacio es de dimensión finita se trata de un espacio euclídeo.

Contenido

1 Definición para espacios euclídeos reales
- 1.1 Propiedades del producto escalar
2 Productos interiores definidos en espacios vectoriales
- 2.1 Definición general
3 Referencias

Definición para espacios euclídeos reales

A • B = |A| |B| cos(θ).
|A| cos(θ) es la proyección escalar de A en B.

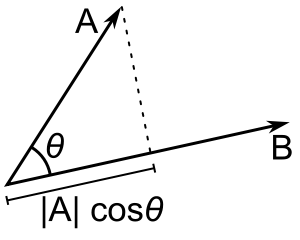
El producto escalar de dos vectores en un espacio euclídeo se define como el producto de sus módulos por el coseno del ángulo $θ$ que forman. El resultado es siempre una magnitud escalar. Se representa por un punto centrado:

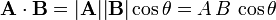
$\mathbf{A} \cdot \mathbf{B}= |\mathbf{A}| |\mathbf{B}| \cos \theta = A \,B \,\cos \theta$

Siendo esta definición de naturaleza puramente geométrica, es independiente del sistema de coordenadas elegido. El producto escalar de dos vectores es un número (escalar) y, si ninguno de los vectores es nulo, dicho producto será un número positivo, nulo o negativo, según que el ángulo formado por los dos vectores (0≤θ≤π) sea agudo, recto u obtuso.

Puesto que A cos θ representa el módulo de la proyección del vector A sobre la dirección del vector B, esto es A cos θ = proy A_B, será

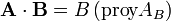
$\mathbf A \cdot \mathbf B = B \left(\text{proy}A _B\right)$

de modo que el producto escalar de dos vectores también puede definirse como el producto del módulo de uno de ellos por la proyección del otro sobre él.

Propiedades del producto escalar

1. Conmutativa:

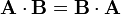
$\mathbf{A} \cdot \mathbf{B}=\mathbf{B} \cdot \mathbf{A}$

2. Distributiva respecto a la suma vectorial:

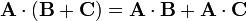
$\mathbf{A}\cdot(\mathbf{B}+\mathbf{C})=\mathbf{A}\cdot\mathbf{B}+\mathbf{A}\cdot\mathbf{C}$

3. Asociativa respecto al producto por un escalar m:

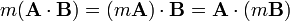
$m (\mathbf{A} \cdot \mathbf{B})= (m\mathbf{A}) \cdot \mathbf{B}=\mathbf{A}\cdot(m\mathbf{B})$

4. Ya que 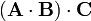$(\mathbf A \cdot \mathbf B)\cdot \mathbf C \,$ no se ha definido (el signo $\cdot \,$ se usa sólo entre vectores) la propiedad asociativa no ha lugar a considerarla. Obsérvese, sin embargo, que en general es

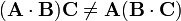
$(\mathbf A \cdot \mathbf B) \mathbf C \neq \mathbf A (\mathbf B \cdot \mathbf C) \,$

5. Si los vectores son ortogonales, su producto escalar es nulo (cos 90º = 0), y viceversa

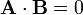
$\mathbf A \cdot \mathbf B = 0 \,$

Esta relación expresa la condición de perpendicularidad entre dos vectores. Obsérvese, que el producto escalar de dos vectores puede ser nulo sin que lo sean uno ni otro vector.

6. En particular, para los vectores unitarios cartesianos tenemos:

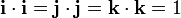
$\mathbf i \cdot \mathbf i = \mathbf j \cdot \mathbf j = \mathbf k \cdot \mathbf k =1 \,$

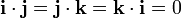
$\mathbf i \cdot \mathbf j = \mathbf j \cdot \mathbf k = \mathbf k \cdot \mathbf i =0 \,$

7. Expresión analítica del producto escalar:

Si los vectores A y B se expresan en función de sus componentes cartesianas rectangulares, o sea,

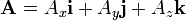
$\mathbf A = A_x\mathbf i+ A_y\mathbf j+A_z\mathbf k \,$

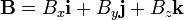
$\mathbf B = B_x\mathbf i+ B_y\mathbf j+B_z\mathbf k \,$

entonces, teniendo en cuenta las propiedades anteriores, se tiene

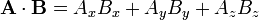
$\mathbf A \cdot \mathbf B = A_xB_x+A_yB_y+A_zB_z\,$

de modo que el producto escalar de dos vectores es igual a la suma de los productos de las componentes cartesianas rectangulares correspondientes.

8. El módulo del vector 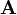$\mathbf A\,$ es:

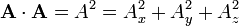
$\mathbf A \cdot \mathbf A = A^2 = A_x^2+A_y^2+A_z^2\,$

o sea

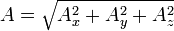
$A = \sqrt{A_x^2+A_y^2+A_z^2} \,$

9. Ángulo formado por dos vectores: De la definición del producto escalar se sigue la expresión

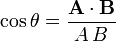
$\cos\theta=\frac{\mathbf A \cdot \mathbf B}{A \, B}$

que nos permite determinar el ángulo formado por dos vectores dados.

10. El producto escalar de dos vectores no tienen operación inversa; esto es, si 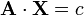$\mathbf A \cdot \mathbf X = c \,$ , no existe una solución única para 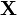$\mathbf X\,$ . Dividir por un vector es una operación sin definir y carente de sentido.

Productos interiores definidos en espacios vectoriales

En el espacio vectorial 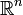$\mathbb{R}^n$ se suele definir el producto interior (llamado, en este caso en concreto, producto punto) por:

$\mathbf{A}\cdot\mathbf{B}=(a_1, a_2, a_3, ..., a_n)\cdot(b_1,b_2,b_3, ..., b_n)=a_1 b_1 + a_2 b_2 + ... a_n b_n$

En el espacio vectorial 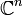$\mathbb{C}^n$ se suele definir el producto interior por:

$\mathbf{A}\cdot\mathbf{B}=(a_1, a_2, a_3, ..., a_n)\cdot(b_1,b_2,b_3, ..., b_n)=a_1 \overline{b_1} + a_2 \overline{b_2} + ... a_n \overline{b_n}$

En el espacio vectorial de las matrices de mxn elementos

$\mathbf{A}\cdot\mathbf{B}=\operatorname{tr} (A \cdot B^T)$

donde tr es la traza de la matriz.

En el espacio vectorial de las funciones continuas sobre el intervalo acotado por a y b (C[a, b])

$\mathbf{f}\cdot\mathbf{g} = \int_{a}^{b} f(x)g(x)\mathrm{d} x$

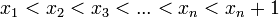Dado $\textstyle [x_1,x_2,x_3,...,x_n,x_n+1] \subseteq \mathbb{R}$ tal que $\textstyle x_1<x_2<x_3<...<x_n<x_n+1 \,$ , en el espacio vectorial de los polinomios de grado menor o igual a n:

$\mathbf{p}\cdot\mathbf{q} = p(x_1)q(x_1)+p(x_2)q(x_2)+...+p(x_n)q(x_n)+p(x_n+1)q(x_n+1)$

De manera similar a como se definen los productos interiores anteriores, se puede definir cualquier otro con la condición de que únicamente debe satisfacer la definición de un producto interior.

Definición general

El producto interior o producto escalar de dos vectores en un espacio vectorial es una forma bilineal, hermítica y definida positiva, por lo que se puede considerar una forma cuadrática definida positiva.

Una operación 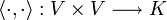$\langle \cdot,\cdot \rangle: V \times V \longrightarrow K$ donde V es el espacio vectorial y K es el cuerpo sobre el que está definido, que tiene que cumplir:

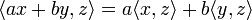$\langle ax+by,z \rangle = a \langle x,z \rangle + b \langle y,z \rangle \,$ (lineal en el primer componente),
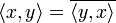$\langle x,y \rangle = \overline{\langle y,x \rangle}$ (hermítica),
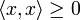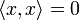$\langle x,x \rangle \geq 0 \,$ , y $\langle x,x \rangle = 0 \,$ si y sólo si x = 0 (definida positiva),

donde x,y,z son vectores arbitrarios, a,b representan escalares cualesquiera y 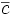$\overline{c}$ es el conjugado del complejo c.

Si el cuerpo tiene parte imaginaria nula (v.g., $\mathbb{R}$ ), la propiedad de ser sesquilineal se convierte en ser bilineal y el ser hermítica se convierte en ser simétrica.

También suele representarse por 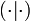$(\cdot|\cdot)$ o por $\bullet$ .

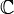Un espacio vectorial sobre el cuerpo $\mathbb{R}$ o $\mathbb{C}$ dotado de un producto escalar se denomina espacio prehilbert o espacio prehilbertiano. Si además es completo, se dice que es un espacio de hilbert, y si la dimensión es finita, se dirá que es un espacio euclídeo.

Todo producto escalar induce una norma sobre el espacio en el que está definido, de la siguiente manera:

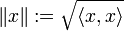$\|x\|:= \sqrt{\langle x,x \rangle}$ .

Referencias

Véase también

Portal:Matemática Contenido relacionado con Matemática.
Portal:Física Contenido relacionado con Física.
Espacio vectorial
Combinación lineal
Sistema generador
Independencia lineal
Matriz de Gram
Base (álgebra)
Base Ortogonal
Base Ortonormal
Coordenadas cartesianas
Producto vectorial
Producto mixto
Producto tensorial

Bibliografía

Ortega, Manuel R. (1989-2006). Lecciones de Física (4 volúmenes) (en español). Monytex. ISBN 84-404-4290-4, ISBN 84-398-9218-7, ISBN 84-398-9219-5, ISBN 84-604-4445-7.
Resnick,Robert & Krane, Kenneth S. (2001). Physics (en inglés). New York: John Wiley & Sons.
Serway, Raymond A.; Jewett, John W. (2004). Physics for Scientists and Engineers, 6ª edición (en inglés), Brooks/Cole. ISBN 0-534-40842-7.
Tipler, Paul A. (2000). Física para la ciencia y la tecnología (2 volúmenes) (en español). Barcelona: Ed. Reverté. ISBN 84-291-4382-3.

Enlaces externos

Obtenido de "Producto escalar"

Categorías: Vectores | Geometría

Wikimedia foundation. 2010.

Игры ⚽ Нужен реферат?

Mira otros diccionarios:

Producto escalar — En matemáticas el producto escalar (también conocido como producto interno o producto punto) es una función definida sobre un espacio vectorial cuyo resultado es una magnitud escalar. El nombre espacio escalar se utiliza para denominar un espacio … Enciclopedia Universal
Triple producto escalar — Saltar a navegación, búsqueda El triple producto escalar es una operación que combina tres vectores en el espacio euclídeo para obtener como resultado un número real, a diferencia del triple producto vectorial que da como resultado un vector. El… … Wikipedia Español
Escalar (matemática) — Saltar a navegación, búsqueda Se denomina escalar a los números reales, complejos o racionales que sirven para describir un fenómeno físico con magnitud, pero sin las características vectoriales de dirección o sentido. Formalmente es un tensor de … Wikipedia Español
Producto vectorial — Saltar a navegación, búsqueda Esquema En álgebra lineal, el producto vectorial es una operación binaria entre dos vectores de un espacio euclídeo tridimensional que da como resultado un vector ortogonal a los d … Wikipedia Español
Producto tensorial — Saltar a navegación, búsqueda En matemáticas, el producto tensorial, denotado por , se puede aplicar en diversos contextos a vectores, matrices, tensores y espacios vectoriales. En cada caso la significación del símbolo es la misma: la operación… … Wikipedia Español
Escalar — Saltar a navegación, búsqueda El término escalar puede referirse a: Escalar, un tipo de magnitud física. Escalar, un espacio vectorial en matemáticas. Un campo escalar. Un producto escalar. La acción del deporte escalada. Pterophyllum scalare o… … Wikipedia Español
Producto mixto — El producto mixto (o también conocido como triple producto escalar) es una operación entre tres vectores que combina el producto escalar con el producto vectorial para obtener un resultado escalar. Contenido 1 Producto punto y producto cruz 2… … Wikipedia Español
Escalar — (Del lat. vulgar scalare, escalera.) ► adjetivo 1 FÍSICA Se aplica a la magnitud física y matemática, como la temperatura o la presión, que se expresan sólo con un número. ► verbo transitivo 2 Subir, trepar o ascender por una montaña, pendiente o … Enciclopedia Universal
Producto — (Del lat. productum.) ► sustantivo masculino 1 Cosa o conjunto de cosas producidas: ■ los productos lácteos son fundamentales para el crecimiento. SINÓNIMO producción 2 MATEMÁTICAS Resultado de una multiplicación: ■ dime el producto de dos por… … Enciclopedia Universal
Producto de Kronecker — Saltar a navegación, búsqueda En matemáticas, se llama producto de Kronecker, denotado con , a una operación sobre dos matrices de tamaño arbitrario que da como resultado una matriz bloque. Es un caso especial del producto tensorial. El producto… … Wikipedia Español

Los diccionarios y las enciclopedias sobre el Académico

Producto escalar

Producto escalar

Contenido