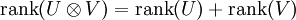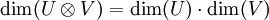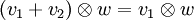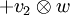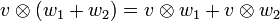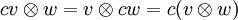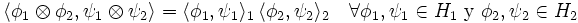- Producto tensorial
-
Producto tensorial
En matemáticas, el producto tensorial, denotado por
 , se puede aplicar en diversos contextos a vectores, matrices, tensores y espacios vectoriales. En cada caso la significación del símbolo es la misma: la operación bilineal más general.
, se puede aplicar en diversos contextos a vectores, matrices, tensores y espacios vectoriales. En cada caso la significación del símbolo es la misma: la operación bilineal más general.Un caso representativo es producto de Kronecker de cualesquiera dos matrices. ejemplo:
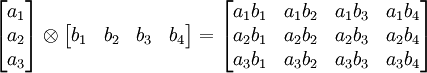
rango resultante = 2, dimensión resultante = 3x4.
Aquí el rango denota el número de índices indispensables, mientras que la dimensión cuenta el número de grados de libertad en el arreglo que resulta.
Definición formal.
Producto tensorial de grupos abelianos.
Sea M y N dos grupos abelianos. Consideramos el grupo abeliano libre
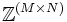 de M y N. Éste grupo abeliano es el formado por aplicaciones
de M y N. Éste grupo abeliano es el formado por aplicaciones 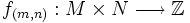 de forma que eventualmente f(m,n) = 0 (i.e., para cada
de forma que eventualmente f(m,n) = 0 (i.e., para cada 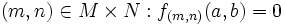 excepto para una cantidad finita de elementos
excepto para una cantidad finita de elementos 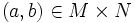 ). Como todo grupo abeliano, podemos considerarlo como
). Como todo grupo abeliano, podemos considerarlo como 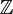 -módulo. Bajo esta óptica, el grupo abeliano libre
-módulo. Bajo esta óptica, el grupo abeliano libre 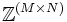 puede expresarse como el conjunto de las combinaciones
puede expresarse como el conjunto de las combinaciones 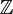 -lineales de los elementos
-lineales de los elementos 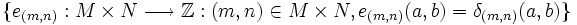 (δ(m,n) es la delta de Kroneker del elemento
(δ(m,n) es la delta de Kroneker del elemento 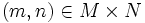 , que es una función
, que es una función 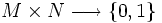 de forma que δ(m,n)(a,b) = 1 si y sólo si m = a y n = b, y 0 en cualquier otro caso). Tomamos ahora el conjunto de los
de forma que δ(m,n)(a,b) = 1 si y sólo si m = a y n = b, y 0 en cualquier otro caso). Tomamos ahora el conjunto de los 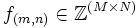 de forma que, cualesquiera que sean
de forma que, cualesquiera que sean 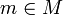 y
y 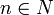 es
es 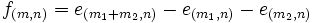 para algunos
para algunos 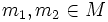 o bien
o bien 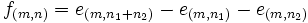 para algunos
para algunos 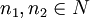 . Denominamos K al subgrupo generado por este conjunto. Es un subgrupo normal (ya que es un subgrupo de un grupo abeliano) de
. Denominamos K al subgrupo generado por este conjunto. Es un subgrupo normal (ya que es un subgrupo de un grupo abeliano) de 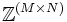 . El producto tensorial de M y N es el grupo cociente
. El producto tensorial de M y N es el grupo cociente 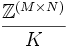 . Se denota por
. Se denota por 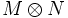 . La clase de equivalencia del elemento e(m,n) se denota
. La clase de equivalencia del elemento e(m,n) se denota 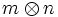 .
.Producto tensorial de módulos.
Sea R un anillo unitario, M un R-módulo a derechas y N un R-módulo a izquierdas. Consideramos el módulo libre
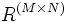 de M y N. Tomamos ahora el conjunto de los
de M y N. Tomamos ahora el conjunto de los 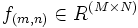 de forma que, cualesquiera que sean
de forma que, cualesquiera que sean 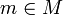 y todo
y todo 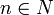 es
es 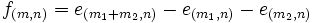 para algunos
para algunos 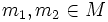 , o bien
, o bien 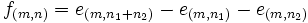 para algunos
para algunos 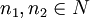 , o bien
, o bien 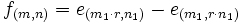 para algunos
para algunos 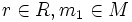 y
y 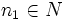 . Denominamos K al submódulo generado por este conjunto. El producto tensorial de M y N es el grupo cociente
. Denominamos K al submódulo generado por este conjunto. El producto tensorial de M y N es el grupo cociente 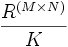 . Se denota por
. Se denota por 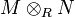 . La clase de equivalencia del elemento e(m,n) se denota
. La clase de equivalencia del elemento e(m,n) se denota 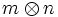 .
.Producto tensorial de dos tensores
Hay una fórmula particular para el producto de dos (o más) tensores
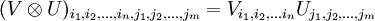 ,
,
donde se esta asumiendo, para simplificar, tensores ortogonales, sin distinción entre índices covariantes y contravariantes.
Los parámetros introducidos arriba trabajan así:
Véase también: Cálculo tensorialProducto tensorial de funciones multilineales
dadas funciones multilineales f(x1... xk) y g(x1... xm) su producto tensorial es la función multilineal
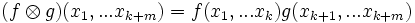
Producto tensorial de espacios vectoriales
El producto
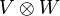 de dos espacios vectoriales V y W tienen una definición formal por el método de generadores y relaciones. La clase de equivalencia de (v, w) se llama un tensor y es denotada por
de dos espacios vectoriales V y W tienen una definición formal por el método de generadores y relaciones. La clase de equivalencia de (v, w) se llama un tensor y es denotada por 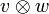 . Por construcción, se puede probar solamente tantas identidades entre los tensores, y las sumas de tensores, como se siguen de las relaciones usadas.
. Por construcción, se puede probar solamente tantas identidades entre los tensores, y las sumas de tensores, como se siguen de las relaciones usadas.Tómese el espacio vectorial generado por W x V y aplique (factorice los subespacios generados por) las relaciones multilineales detalladas abajo. Con esta notación las relaciones toman la forma:
- cada elemento del producto tensorial es una suma finita de tensores: más de un tensor se requiere generalmente para hacer eso. Se muestra simplemente cómo construir una base de los
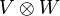 .
.
Dadas bases para V y W, el conjunto de productos tensoriales de los vectores de base, uno de V y uno de W, formas una base para
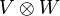 .
.La dimensión del producto tensorial por lo tanto es el producto de dimensiones.
Propiedad universal del producto tensorial
Sea G un grupo abeliano, R un anillo unitario, M un R-módulo a derechas, N un R-módulo a izquierdas y
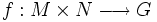 una aplicación R-equilibrada (si M y N los consideramos sólo como grupos abelianos, entonces
una aplicación R-equilibrada (si M y N los consideramos sólo como grupos abelianos, entonces 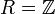 ; si fuesen M y N espacios vectoriales, entonces R sería un cuerpo, si M y N fuesen espacios vectoriales reales, sería
; si fuesen M y N espacios vectoriales, entonces R sería un cuerpo, si M y N fuesen espacios vectoriales reales, sería 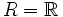 ). Existe un único homomofismo de grupos
). Existe un único homomofismo de grupos 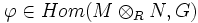 de manera que
de manera que 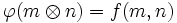 , cualesquiera que sean
, cualesquiera que sean 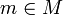 y
y 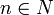 .
.Particularización a espacios vectoriales reales.
El espacio de todos las funciones bilineales desde V x W a R es naturalmente isomorfo al espacio de todos las funciones lineales de
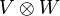 a R. Esto es por construcción:
a R. Esto es por construcción: 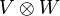 tienen solamente las relaciones que son necesarias para asegurarse de que un homomorfismo de los
tienen solamente las relaciones que son necesarias para asegurarse de que un homomorfismo de los 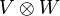 a R será bilineal.
a R será bilineal.Producto tensorial de espacios de Hilbert
El producto tensorial de dos espacios de Hilbert es otro espacio de Hilbert, que se define según lo descrito abajo.
Definición
Sean H1 y H2 dos espacios de Hilbert con los productos internos < ·, ·>1 y < ·, ·>2, respectivamente. Constrúyase el producto tensorial de H1 y H2 como espacios vectoriales según lo explicado arriba. Podemos convertir a este producto tensorial de espacios vectoriales en uno con producto escalar definiendo:
y extendiendo por linealidad. Finalmente, tomemos completación de este producto interno. El resultado es el producto tensorial de H1 y H2 como espacios de Hilbert.
Propiedades
Si H1 y H2 tienen bases ortonormales {φk} y {ψl}, respectivamente, entonces {φk⊗ψl} son una base ortonormal para H1⊗H2.
Ejemplos y aplicaciones
Los ejemplos siguientes muestran que los productos tensoriales se presentan naturalmente.
Dados dos espacios de medida X y Y, con μ y ν las medidas respectivamente, uno puede considerar L²(X × Y), el espacio de las funciones en X × Y que son cuadrado-integrables con respecto a la medida producto μ × ν. Si f es una función cuadrado-integrable en X, y g es una función cuadrado-integrable en Y, entonces podemos definir una función h en X × Y por h(x, y) = f(x) g(y). la definición de la medida producto nos asegura que todas las funciones de esta forma son cuadrado-integrables, así que ésta define una función bilineal de L²(X) × L²(Y) → L²(X × Y). Las combinaciones lineales de las funciones de la forma f(x) g(y) están también en L²(X × Y). Resulta que el conjunto de combinaciones lineales es de hecho denso en L²(X × Y), si L²(X) y L²(Y) son separables. Esto demuestra que L²(X) ⊗ L²(Y) es isomorfo a L²(X × Y), y también explica porqué necesitamos tomar la completación en la construcción del producto tensorial del espacio de Hilbert.
Semejantemente, podemos demostrar que L²(X; H), denotando el espacio de las funciones cuadrado-integrables de X → H, es isomorfo al L²(X) ⊗ H si este espacio es separable. El isomorfismo manda f(x) ⊗ψ ∈ L²(X)⊗ H a f(x)ψ ∈ L²(X; H). Podemos combinar esto con el ejemplo anterior y concluir que L²(X) ⊗ L²(Y) y L²(X × Y) son ambos isomorfos a L²(X; L²(Y)).
Los productos tensoriales de los espacios de Hilbert preséntanse a menudo en la mecánica cuántica. Si una cierta partícula es descrita por el espacio de Hilbert H1, y se describe otra partícula por H2, entonces el conjunto que consiste en ambas partículas es descrito por el producto tensorial de H1 y H2. Por ejemplo, el espacio de estado de un oscilador armónico cuántico es L²(R), así que el espacio de estado de dos osciladores es L²(R) ⊗ L²(R ), el cual es isomorfo a L²(R²). Por lo tanto, el conjunto de la dos partículas es descrito por las funciones de la onda de la forma φ(x1, x2). Un ejemplo más intrincado es proporcionado por los espacios de Fock, que describen un número variable de partículas.
Descripción intrínseca
En álgebra abstracta, el álgebra lineal es elevada a álgebra multilineal introduciendo el producto tensorial de dos espacios vectoriales. Se lo introduce para reducir el estudio de los operadores bilineales al de los operadores lineales. Esto es suficiente para hacer lo mismo con todos las funciones multilineales.
Formalmente, el producto tensorial de los dos espacios vectoriales V y W sobre el mismo cuerpo base F es definido por la siguiente propiedad universal: es un espacio vectorial T sobre F, junto con un operador bilineal:
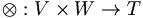 , tales que para cada operador bilineal
, tales que para cada operador bilineal 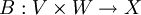 existe un operador lineal L único: L: T → X con
existe un operador lineal L único: L: T → X con 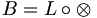 , i.e.
, i.e. 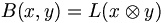 para todo x en V y y en W.
para todo x en V y y en W.El producto tensorial es único salvo isomorfismo, especificado unívocamente por este requisito, y podemos por lo tanto escribir
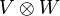 en vez de T. Por la construcción directa, según lo sugerido en la sección anterior, uno puede demostrar que existe el producto tensorial para cualesquiera dos espacios vectoriales. El espacio
en vez de T. Por la construcción directa, según lo sugerido en la sección anterior, uno puede demostrar que existe el producto tensorial para cualesquiera dos espacios vectoriales. El espacio 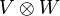 es generado por la imagen de la
es generado por la imagen de la 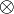 y aún más: si S es una base de V y T es una base de W, entonces los
y aún más: si S es una base de V y T es una base de W, entonces los 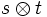 (tal que
(tal que 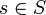 y
y 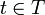 ) son una base para
) son una base para 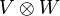 .
.La dimensión del espacio por lo tanto está dada por el producto de las dimensiones de V y de W. Es posible generalizar la definición a un producto tensorial de cualquier número de espacios. Por ejemplo, la propiedad universal de
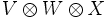 es que cada operador tri-lineal en
es que cada operador tri-lineal en 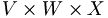 corresponde a un operador lineal único en
corresponde a un operador lineal único en 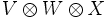 .
.El producto binario tensorial es asociativo:
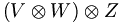 es naturalmente isomorfo a
es naturalmente isomorfo a 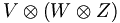 .
.El producto tensorial de los tres se puede por lo tanto identificar con cualquiera de ésos: el binario
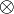 será suficiente. Los espacios tensoriales permiten que utilicemos la teoría de operadores lineales para estudiar operadores multilineales, donde el caso bilineal es el principal.
será suficiente. Los espacios tensoriales permiten que utilicemos la teoría de operadores lineales para estudiar operadores multilineales, donde el caso bilineal es el principal.Relación con el espacio dual
Nótese que el espacio
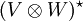 (espacio dual de
(espacio dual de 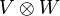 que contiene todos los funcionales lineales en ese espacio) corresponde naturalmente al espacio de todos los funcionales bilineales en los
que contiene todos los funcionales lineales en ese espacio) corresponde naturalmente al espacio de todos los funcionales bilineales en los 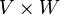 . Es decir cada funcional bilineal es un funcional en el producto tensorial, y viceversa. Cuando los espacios V y W son de dimensión finita, existe un isomorfismo natural entre
. Es decir cada funcional bilineal es un funcional en el producto tensorial, y viceversa. Cuando los espacios V y W son de dimensión finita, existe un isomorfismo natural entre 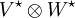 y
y 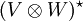 . Así pues, los tensores de los funcionales lineales son funcionales bilineales. Esto nos da una nueva manera de mirar el espacio de funcionales bilineales: como producto tensorial. En el caso de dimensión arbitraria, tan sólo tenemos la inclusión
. Así pues, los tensores de los funcionales lineales son funcionales bilineales. Esto nos da una nueva manera de mirar el espacio de funcionales bilineales: como producto tensorial. En el caso de dimensión arbitraria, tan sólo tenemos la inclusión 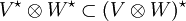 .
.Tipos de tensores, v.g. alternantes
Los subespacios lineales de operadores bilineales (o en general, operadores multilineales) determinan espacios cociente naturales del espacio tensorial, que son con frecuencia útiles. Vea producto cuña para el primer ejemplo principal. Otro sería el tratamiento de las formas algebraicas como tensores anti-simétricos.
Sobre anillos más generales
Es también posible generalizar la definición a los productos tensoriales de módulos sobre el mismo anillo. Si el anillo es no conmutativo, necesitaremos tener cuidado en distinguir los módulos derechos y los módulos izquierdos. Escribiremos RM para un módulo izquierdo, y MR para un módulo derecho. Si un módulo M tiene una estructura izquierda de módulo sobre un anillo R y una estructura de módulo derecho sobre un anillo S, y además para cada m en M, r en R y s en S tenemos r(ms) = (rm)s, entonces diremos que M es un bimódulo, y lo notaremos RMS. Nótese que cada módulo izquierdo es un bimódulo con Z actuando por mn = m + m +... +m de m como el anillo derecho, y viceversa.
Al definir el producto tensorial, necesitamos ser cuidadosos respecto al anillo: la mayoría de los módulos se pueden considerar como distintos módulos sobre diversos anillos o sobre el mismo anillo con diversas acciones del anillo en los elementos del módulo. La forma más general de la definición de producto tensorial es como sigue: Sea MR y RN un módulo derecho y un módulo izquierdo, respectivamente. Su producto tensorial R es un grupo abeliano P junto con un operador R-bilineal T: M x N → P tal que para cada operador R-bilineal B: M x N → O hay un homomorfismo de grupos único L: P → O tales que L o T = B. P no necesita ser un módulo sobre R. Sin embargo, si S1MR es un S1-R-bimódulo, entonces hay una única estructura de S1-módulo izquierdo en P que es compatible con T. similarmente RMS2 es un R-S2-bimódulo, entonces semejantemente hay una única estructura de S2-módulo derecho en P que es compatible con T. Si M y N son ambos bimódulos, entonces P es también un bimódulo, otra vez de una manera única. (P, T) es único salvo un isomorfismo único, y se llama el "producto tensorial" de M y N. Si R es un anillo, RM es un R-módulo izquierdo, y el conmutador rs-sr de cualesquiera dos elementos r y s de R está en el anulador de M, entonces se puede hacer de M un módulo derecho de R fijando mr=rm. Observe que en esta situación la acción de R en M factoriza por una acción del anillo comutativo R/Z(R), i.e. R módulo su centro. En este caso el producto tensorial de M con sí mismo sobre R es otra vez un R-módulo. Si M y N es ambos R-módulos que satisfacen esta condición, entonces su producto tensorial es otra vez un R-módulo. Esto es una técnica muy común en álgebra comutativa.
Ejemplo: Considere los números racionales Q y los enteros módulo n Zn. Ambos se pueden considerar como módulos sobre los números enteros, Z. Sea B: Q x Zn → M sea un operador Z-bilineal. Entonces B(q, i) = B(q/n, n*i) = B(q/p, 0) = 0, así que cada operador bilineal es idénticamente cero. Por lo tanto, si definimos P como el módulo trivial, y T como la función bilineal cero, entonces las propiedades para el producto tensorial son satisfechas. Por lo tanto, el producto tensorial de Q y Zn es {0}.
Temas relacionados
- Espacio vectorial
- Combinación lineal
- Sistema generador
- Independencia lineal
- Base (álgebra)
- Base Ortogonal
- Base Ortonormal
- Coordenadas cartesianas
- Producto escalar
- Producto vectorial
- Producto mixto
- Potencia tensorial
Categorías: Álgebra | Álgebra multilineal
Wikimedia foundation. 2010.