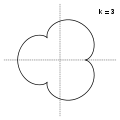
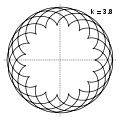
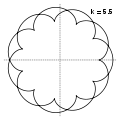
Epicicloide

Epicicloide

Epicicloide

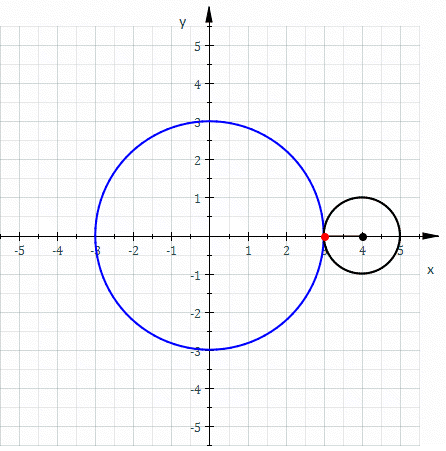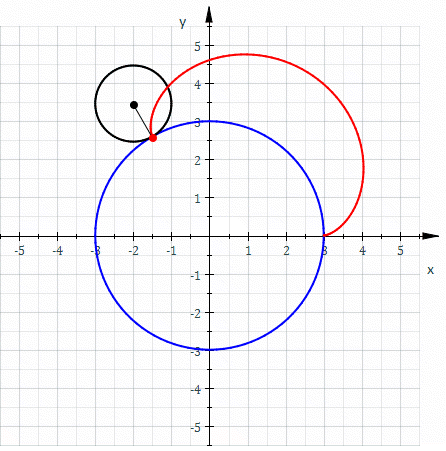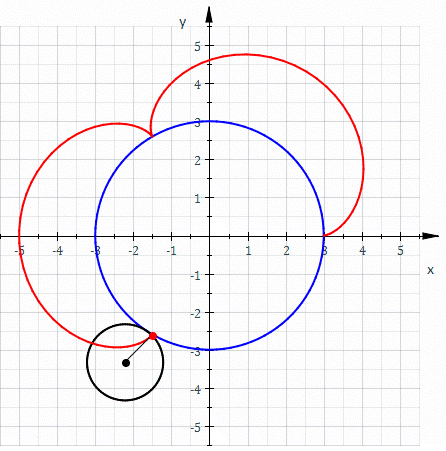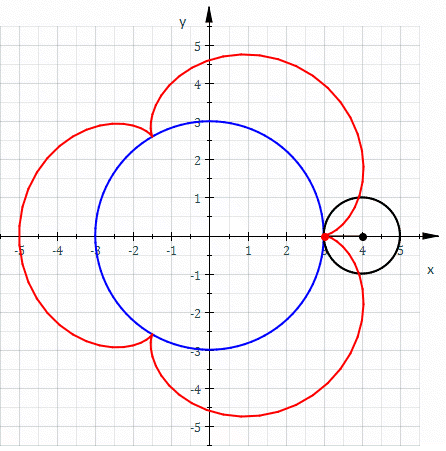La curva roja es una epicicloide trazada a medida que el pequeño círculo (radio r = 1) gira sobre la circunferencia de un círculo mayor (radius R = 3).

La epicicloide es la curva generada por la trayectoria de un punto de una circunferencia que rueda, sin deslizamiento, por el exterior de otra circunferencia directriz. Es un tipo de ruleta cicloidal.

Contenido

Ecuación

Epicicloide.png

Considerando la figura podemos escribir:

x=(r_1+r_2)sen\ \alpha\ - r_2\ cos \gamma

y=(r_1+r_2)cos\ \alpha\ + r_2\ sen \gamma

con γ = α + β − π / 2 y, además, como la circunferencia rueda sin deslizamiento, los arcos l1 y l2 son iguales, i.e: r_1\ \alpha =l_1=l_2=r_2\ \beta. De aquí se tiene que \beta = \frac {r_1}{r_2} \alpha

Sustituyendo β y γ en las ecuaciones [1] y [2] tenemos la ecuación paramétrica de la epicicloide: x=(r_1+r_2)sen\ \alpha\ -r_2\ sen\ [\alpha (1+\frac {r_1}{r_2})]

y=(r_1+r_2)cos\ \alpha\ -r_2\ cos\ [\alpha (1+\frac {r_1}{r_2})]

Casos particulares

Cuando \frac {r_1}{r_2} es un número racional, i.e., k = \frac {r_1}{r_2}=\frac {p}{q}, siendo p y q números enteros, las epicicloides son curvas algebraicas.

Cuando r1=r2, i.e, k = 1 tenemos el cardioide

Si \frac {r_1}{r_2} es irracional, la curva es trascendente y cubre completamente la región entre los radios r1 y r2.

Ejemplos

ejemplos de epicicloides

k=1

k=2

k=3

k=4

k=2.1=21/10

k=3.8=19/5

k=5.5=11/2

k=7.2=36/5

Véase también

Referencias en la Web

Obtenido de "Epicicloide"

Wikimedia foundation. 2010.

Игры ⚽ Нужна курсовая?

Mira otros diccionarios:

  • epicicloide — (De epi y cicloide). f. Geom. Curva descrita por un punto dado de una circunferencia al rodar esta sobre el exterior de otra fija. epicicloide esférica. f. Geom. La descrita cuando los planos de las dos circunferencias forman un ángulo constante …   Diccionario de la lengua española

  • epicicloide — ► sustantivo femenino 1 GEOMETRÍA Línea curva descrita por un punto de una circunferencia que rueda sobre sobre otra fija, siendo ambas tangentes exteriormente. SINÓNIMO [epicicloide plana] FRASEOLOGÍA epicicloide esférica GEOMETRÍA La descrita… …   Enciclopedia Universal

  • epicicloide — e·pi·ci·clòi·de s.f. TS geom. curva piana descritta da un punto di un cerchio che ruota sulla circonferenza esterna di un altro cerchio fisso; anche agg.: curva epicicloide {{line}} {{/line}} DATA: 1715 18. ETIMO: der. di 1cicloide con epi …   Dizionario italiano

  • epicicloide — {{hw}}{{epicicloide}}{{/hw}}s. f. Curva descritta da un punto di una circonferenza che rotoli senza strisciare su un altra circonferenza …   Enciclopedia di italiano

  • epicicloide — pl.m. e f. epicicloidi …   Dizionario dei sinonimi e contrari

  • epicicloide esférica — ► locución GEOMETRÍA La descrita cuando los dos planos de las circunferencias forman un ángulo constante …   Enciclopedia Universal

  • Curva cíclica — Saltar a navegación, búsqueda Una curva cíclica es la generada por el movimiento de un punto vinculado a una circunferencia (o recta) que rueda sobre otra circunferencia (o recta) sin resbalar . Se denomina curva directriz o base a la considerada …   Wikipedia Español

  • Cardioide — Saltar a navegación, búsqueda Cardioide Se llama cardioide a la curva cuya ecuación polar es: ρ=a(1+cos θ), por su semejanza con el dibujo de un corazón. La cardioide es una curva ruleta del tipo epicicloide, con k=1; pero también es un caracol… …   Wikipedia Español

  • Engranaje — Animación de dos engranajes. Piñón y corona …   Wikipedia Español

  • Ruleta (geometría) — Saltar a navegación, búsqueda Ruleta, en matemática, se denomina a la curva plana que describe la trayectoria de un punto, vinculado a una curva generatriz C1, que rueda sobre otra curva directriz C2, tangencialmente, sin deslizamiento. Tanto C1… …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”