Curva cíclica

Curva cíclica

Curva cíclica

Una curva cíclica es la generada por el movimiento de un punto vinculado a una circunferencia (o recta) que rueda sobre otra circunferencia (o recta) sin "resbalar". Se denomina curva directriz o "base" a la considerada fija. En general, dadas dos circunferencias, si consideramos fija una de ellas y se hace rodar otra sobre la fija, los puntos vinculados a la móvil describen curvas cíclicas.

Cicloide.
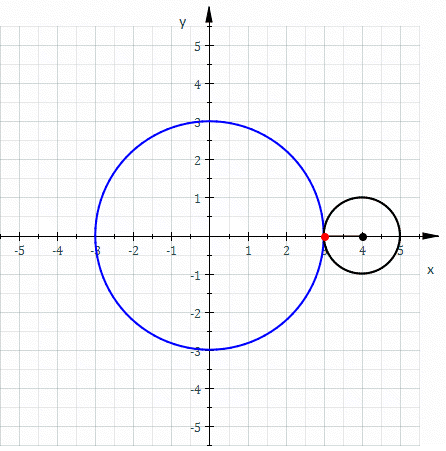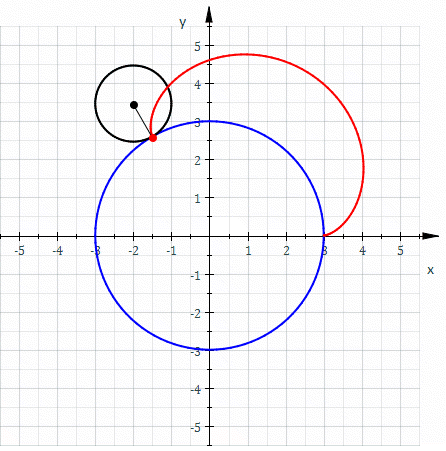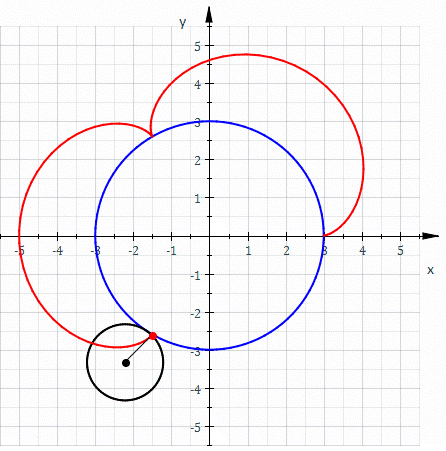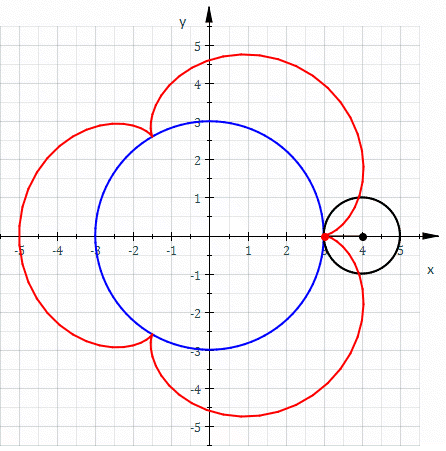Epicicloide (R=3, r=1).
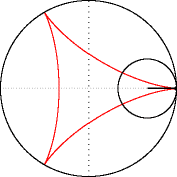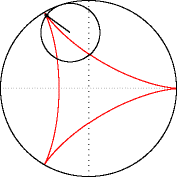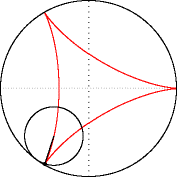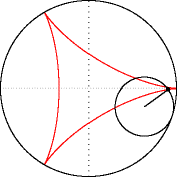Hipocicloide (R=3, r=1).

Clasificación de las curvas cíclicas

Si la directriz es una línea recta:

  • Cicloide:
    • normal, si el punto generador está en la circunferencia que rueda.
    • alargada, si el punto generador está fuera de la circunferencia que rueda.
    • acortada, si el punto generador está dentro de la circunferencia que rueda.

Si la directriz es una circunferencia:

  • Epicicloide, si la circunferencia que rueda es exterior:
    • normal,
    • alargada,
    • acortada.
  • Hipocicloide, si la circunferencia que rueda es interior,
    • normal,
    • alargada,
    • acortada.

También son curvas cíclicas:

  • Envolvente de la circunferencia.
  • Pericicloide.
  • Hélice:
    • cilíndrica,
    • cónica,
    • esférica.

Definición matemática

Una curva cíclica puede definirse mediante dos ecuaciones intrínsecas:


\left[ 1 \right] \quad R_c^2+ \omega ^2 s^2= \omega ^2 A^2
\left[ 2 \right] \quad s=A sin( \omega \phi )\,

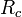donde R_c\, representa el radio de curvatura y s\, la abscisa de la curva:

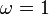\omega = 1\, : cicloide (A = 4 veces el radio del círculo de rodadura)
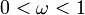0 < \omega < 1\, : epicicloide ( 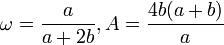\omega = \frac{a}{a+2b}, A = \frac{4b(a+b)}{a}\, (donde está el radio del círculo base, b del círculo de rodadura)
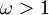\omega > 1\, : hipocicloide ( 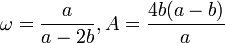\omega = \frac{a}{a-2b}, A = \frac{4b(a-b)}{a}\, (donde está el radio del círculo base, b del círculo de rodadura).

Enlaces externos

Obtenido de "Curva c%C3%ADclica"

Wikimedia foundation. 2010.

Игры ⚽ Нужен реферат?

Mira otros diccionarios:

  • ciclica — cì·cli·ca s.f. 1. TS mat. curva sghemba del quarto ordine e di prima specie, situata su di una superficie sferica 2. OB TS astron. linea che si suppone descrivano gli astri nei loro movimenti {{line}} {{/line}} DATA: 1830 nell accez. 2. ETIMO:… …   Dizionario italiano

  • Antananarivo — Tananarive Antananarivo Bandera de Antananarivo Bandera Escudo …   Wikipedia Español

  • San Antonio Oeste — Saltar a navegación, búsqueda San Antonio Oeste …   Wikipedia Español

  • Límite de fatiga — Curva S N mediante la cual se puede calcular el límite de fatiga. Para la mayoría de los metales existe un esfuerzo crítico, por debajo del cual la rotura sólo se produce al cabo de un considerable período o número de ciclos. Dicho esfuerzo… …   Wikipedia Español

  • Integración — La integral definida de una función representa el área limitada por la gráfica de la función, con signo positivo cuando la función toma valores positivos y negativo cuando toma valores negativos. Para otros usos de este término, véase Integración …   Wikipedia Español

  • Fatiga de materiales — Saltar a navegación, búsqueda En ingeniería y, en especial, en ciencia de materiales, la fatiga de materiales se refiere a un fenómeno por el cual la rotura de los materiales bajo cargas dinámicas cíclicas (fuerzas repetidas aplicadas sobre el… …   Wikipedia Español

  • Principio de acción — Saltar a navegación, búsqueda Para otros usos de la palabra acción, véase Acción. En física, el principio de acción es una aserción sobre la naturaleza del movimiento o trayectoria de un objeto o más generalmente la evolución temporal de un… …   Wikipedia Español

  • Hemodinámica — La hemodinámica es aquella parte de la cardiología que se encarga del estudio anatómico y funcional del corazón mediante la introducción de catéteres finos a través de las arterias de la ingle o del brazo. Esta técnica conocida como cateterismo… …   Wikipedia Español

  • Plaga de topillos en Castilla y León de 2007 — Saltar a navegación, búsqueda Topillo en ple …   Wikipedia Español

  • Epidemia — Saltar a navegación, búsqueda La Epidemia de cólera en Londres en 1854 fue estudiada por Dr. John Snow que realizó este mapa y que supuso el primer estudio epidemiológico. Los puntos muestran los casos de muerte. Las cruces representan los pozos… …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”