Esfera homológica

Esfera homológica

Esfera homológica

En la topología algebraica, una esfera homológica M es una n-variedad cuyos grupos de homología son iguales a los de la esfera de la dimensión correspondiente. Esto quiere decir que

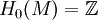
  • H_0(M)=\mathbb{Z}
  • H1(M) = {0}
  • ...
  • Hn − 1(M) = {0}
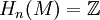  • H_n(M)=\mathbb{Z}.

Aunque la definición no depende de la dimensión, las esferas homológicas se suelen considerar sobre todo en topología de 3-variedades: De hecho, la primera versión de la conjetura de Poincaré fue, que la única 3-esfera homológica es la esfera estandar. Poincaré logro desmentir su conjetura al encontrar un contra-ejemplo. Éste - ahora conocido como la esfera de Poincaré o espacio dodecaédrico de Poincaré - es una 3-variedad cuyo grupo fundamental es de orden 120.

La 3-esfera S3 y la esfera de Poincaré son las únicas esferas homológicas tridimensionales con grupo fundamental finito.

Obtenido de "Esfera homol%C3%B3gica"

Wikimedia foundation. 2010.

Игры ⚽ Нужна курсовая?

Mira otros diccionarios:

  • Esfera — Para otros usos de este término, véase Esfera (desambiguación). Proyección en dos dimensiones de una esfera definida mediante paralelos y meridianos. En geometría, una esfera es un cuerpo geométrico limitado por una superficie curva cerrada cuyos …   Wikipedia Español

  • 3-esfera — Proyección estereográfica de los paralelos de una hiperesfera (rojo), los meridianos (azul) y los hipermeridianos (verde). Debido a la propiedad conforme de la proyección estereográfica, todas estas curvas se intersecan unas a otras… …   Wikipedia Español

  • Topología geométrica — La topología geométrica (topología de dimensiones bajas) es el área de la topología y la topología algebraica que estudia problemas geométricos, topológicos y algebraicos que surgen en el estudio de variedades de dimensiones menores que 5,… …   Wikipedia Español

  • Homología — puede referirse a: Homología (biología), la relación que existe entre dos partes orgánicas diferentes cuando sus determinantes genéticos tienen el mismo origen evolutivo. Homología (geometría), transformación biyectiva del plano proyectivo en sí… …   Wikipedia Español

  • Elipsoide — Saltar a navegación, búsqueda Un elipsoide es una superficie curva cerrada cuyas tres secciones ortogonales principales son elípticas, es decir, las originadas por planos que contienen dos ejes cartesianos. En matemáticas, es una cuádrica análoga …   Wikipedia Español

  • Geometría algebraica — La geometría algebraica es una rama de la matemática que, como sugiere su nombre, combina el álgebra abstracta, especialmente el álgebra conmutativa, con la geometría. Se puede comprender como el estudio de los conjuntos de soluciones de los… …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”