- Estado mezcla
-
Estado mezcla
En mecánica cuántica se llama estado mezcla, por contraposición a un estado puro, aquél que no está máximamente determinado. En otras palabras; si midiéramos más refinadamente los sistemas individuales que forman la colectividad estadística que en principio pensábamos constaba de elementos idénticos (con todos sus atributos físicos idénticos dentro de las limitaciones que impone el principio de incertidumbre), veríamos que hay características más finas que los diferencian. La explicación intuitiva de esto es que estamos mezclando (deliberadamente o no) colectividades estadísticas que podrían considerarse como estados puros (máximamente determinados) diferentes.
Una analogía evidente sería que se nos presentara una estadística de, por ejemplo, las estaturas de los europeos. Todas las propiedades de esta estadística están contenidas en la distribución de probabilidad p(h), donde h es la estatura. Alguien podría facilitarnos información adicional especificando unas distribuciones de probabilidad más detalladas p(N,h), donde N es la nacionalidad. Pues bien, la distribución de probabilidad p(h) sería una mezcla de las distintas p(N,h) en el mismo sentido que pretendemos precisar aquí.
Contenido
Motivación y antecedentes históricos
El concepto de estado mezcla fue introducido en 1927 independientemente por el físico soviético Lev Davidovich Landau y Felix Bloch y matemáticamente formulado en términos del operador densidad por John Von Neumann. En el caso de Landau, se trataba de dar un enfoque a la mecánica cuántica más acorde con las exigencias de la física estadística, en particular con vistas a considerar el comportamiento cuántico de sistemas complejos (formados por grandes números de partículas en interacción mutua), como gases o cristales. En el caso de Von Neumann, la motivación era la de dotar de mayor rigor a la estructura lógica y matemática de la mecánica cuántica; más en particular, y en lo que atañe a los estados mezcla, la formulación de unos requisitos mínimos que definan el estado cuántico.
Formulación matemática
El operador densidad
En mecánica cuántica un sistema físico que se halla en un estado mezcla no se describe con un único vector de estado, sino que hay que asignarle un operador en el espacio de Hilbert de los estados:
La lectura intuitiva de esta fórmula es que el sistema se encuentra en una mezcla de los distintos subestados estadísticos
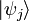 , y cada uno de ellos aparece en la colectividad total con un peso estadístico igual a pj.
, y cada uno de ellos aparece en la colectividad total con un peso estadístico igual a pj.El valor esperado de un observable representado por el operador autoadjunto
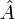 es ahora:
es ahora:Es decir, se trata de la media pesada con probabilidades respectivas pj de cada uno de los valores esperados respectivos en los estados
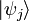 del mismo observable.
del mismo observable.Estados mezcla estrictos
- ρ2 < ρ
Estados puros
- ρ2 = ρ
Véase también
Categoría: Mecánica cuántica
Wikimedia foundation. 2010.

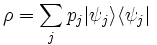
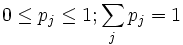
![\langle \hat{A} \rangle_\rho = \operatorname{Tr}[\rho \hat{A}]=\sum_j p_j\langle \psi_j|\hat{A}|\psi_j\rangle](/pictures/eswiki/101/ef0b8d5a8d6e5465695d15100eec2ef8.png)