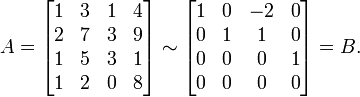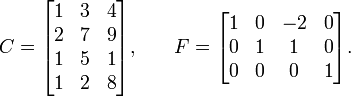Factorización de rango

Factorización de rango

Factorización de rango

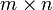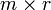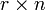Dada una matriz A, de dimensiones m \times n y de rango r, una descomposición de rango de A es un producto A = CF, donde C es una matriz m \times r y F es una matriz r \times n.

Para construir una factorización de este tipo se puede calcular B, la forma escalonada reducida de A. Entonces C se obtiene eliminando de A todas las columnas que no son columnas pivote, y F eliminando todas las filas de ceros de B.

Ejemplo

Considérese la matriz

A = \begin{bmatrix} 1 & 3 & 1 & 4 \\ 2 & 7 & 3 & 9 \\ 1 & 5 & 3 & 1 \\ 1 & 2 & 0 & 8 \end{bmatrix}\sim \begin{bmatrix} 1 & 0 & -2 & 0 \\ 0 & 1 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 \end{bmatrix}=B\text{.}

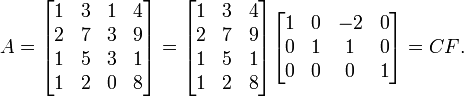
B está en forma escalonada reducida. Entonces C se obtiene eliminando la tercera columna de A, la única que no es columna pivote, y F eliminando la última fila de ceros, de modo que

C = \begin{bmatrix} 1 & 3 & 4 \\ 2 & 7 & 9 \\ 1 & 5 & 1 \\ 1 & 2 & 8 \end{bmatrix}\text{,}\qquad F = \begin{bmatrix} 1 & 0 & -2 & 0 \\ 0 & 1 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}\text{.}

Es inmediato comprobar que

A = \begin{bmatrix} 1 & 3 & 1 & 4 \\ 2 & 7 & 3 & 9 \\ 1 & 5 & 3 & 1 \\ 1 & 2 & 0 & 8 \end{bmatrix} = \begin{bmatrix} 1 & 3 & 4 \\ 2 & 7 & 9 \\ 1 & 5 & 1 \\ 1 & 2 & 8 \end{bmatrix}\begin{bmatrix} 1 & 0 & -2 & 0 \\ 0 & 1 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} = CF\text{.}

Demostración

Sea P una matriz 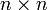n\times n de permutación tal que AP = (C,D) en en forma de bloques, donde las columnas de C son las r columnas pivote de A. Cada columna de D es una combinación lineal de las columnas de C, luego hay una matriz G tal que D = CG, donde las columnas de G contienen los coeficientes de cada una de esas combinaciones lineales. Así pues, AP = (C,CG) = C(Ir,G), siendo Ir la matriz identidad 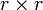r\times r. Mostraremos a continuación que (Ir,G) = FP.

Transformar AP en su forma escalonada reducida equivale a multiplicar por la izquierda por una matriz E que es un producto de matrices elementales, con lo que EAP = BP = EC(Ir,G), donde 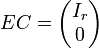EC=\begin{pmatrix} I_r \\ 0 \end{pmatrix}. Podemos entonces escribir 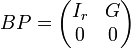BP=\begin{pmatrix} I_r & G \\ 0 & 0 \end{pmatrix}, lo que nos permite identificar (Ir,G) = FP, es decir, las r filas no nulas de la forma escalonada reducida, con la misma permutación de columnas que aplicamos a la matriz A. Tenemos, por tanto, que AP = CFP, y como P es invertible, esto implica que A = CF, lo que completa la prueba.

Referencias

  • Lay, David C. (2005), Linear Algebra and its Applications (3rd edición), Addison Wesley, ISBN 978-0201709704 
  • Golub, Gene H.; Van Loan, Charles F. (1996), Matrix Computations, Johns Hopkins Studies in Mathematical Sciences (3rd edición), The Johns Hopkins University Press, ISBN 978-0801854149 
  • Stewart, Gilbert W. (1998), Matrix Algorithms. I. Basic Decompositions, SIAM, ISBN 978-0-898714-14-2 
Obtenido de "Factorizaci%C3%B3n de rango"

Wikimedia foundation. 2010.

Игры ⚽ Нужна курсовая?

Mira otros diccionarios:

  • Número primo — Un número primo es un número natural mayor que 1, que tiene únicamente dos divisores distintos: él mismo y el 1. Se contraponen así a los números compuestos, que son aquellos que tienen algún divisor natural aparte de sí mismos y del 1. El número …   Wikipedia Español

  • Complejidad y criptografía — La criptografía es la ciencia encargada del estudio y diseño de sistemas que permiten ocultar información. Desde sus inicios, esta capacidad de encubrimiento se ha basado en la dificultad que supondría a una entidad no autorizada el obtener la… …   Wikipedia Español

  • RSA — En criptografía, RSA (Rivest, Shamir y Adleman) es un sistema criptográfico de clave pública desarrollado en 1977. Es el primer y más utilizado algoritmo de este tipo y es válido tanto para cifrar como para firmar digitalmente. La seguridad de… …   Wikipedia Español

  • Sucesión de Sylvester — Demostración gráfica de la convergencia de la suma a 1. Cada fila de k cuadrados de lado tiene un área total de , y todos los cuadra …   Wikipedia Español

  • Curva elíptica — Saltar a navegación, búsqueda En matemáticas, las curvas elípticas se definen mediante ecuaciones cúbicas (de tercer grado). Han sido usadas para probar el último teorema de Fermat y se emplean también en criptografía (para más detalles ver el… …   Wikipedia Español

  • Emmy Noether — Amalie Emmy Noether Nacimiento 23 de marzo de 1882 Erlangen, Baviera, Alemania Fallecimiento …   Wikipedia Español

  • Función zeta de Riemann — ζ(s) en el plano complejo. El color de un punto s codifica el valor de ζ(s): Colores fuertes denotan valores cercanos a 0 y el tono codifica el valor del argumento. El punto blanco en s=1 es el polo de la función zeta; los puntos negros en el eje …   Wikipedia Español

  • Algoritmo de la división — Se ha sugerido que Algoritmo de la división sea fusionado en este artículo o sección (discusión). Una vez que hayas realizado la fusión de artículos, pide la fusión de historiales aquí. En matemáticas, y más precisamente en la aritmética, la… …   Wikipedia Español

  • Computación cuántica — La esfera de Bloch es una representación de un qubit, el bloque de construcción fundamental de los computadores cuánticos. La computación cuántica es un paradigma de computación distinto al de la computación clásica. Se basa en el uso de qubits… …   Wikipedia Español

  • División euclídea — Saltar a navegación, búsqueda La división euclidiana (o euclídea) del entero a por el entero no nulo b es el cálculo que permite encontrar los enteros q y r tales que: a = bq + r,     con  0 ≤ r < |b| a se llama el… …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”