La división euclidiana (o euclídea) del entero a por el entero no nulo b es el cálculo que permite encontrar los enteros q y r tales que:

a = bq + r,     con  0 ≤ r < |b|

a se llama el dividendo, b el divisor, q el cociente y r el resto.

La división euclidiana es la división entre enteros, con resto, que se enseña en los colegios (a alumnos de aproximadamente siete años), como introducción a la división exacta de los números reales.

Contenido 1 Ejemplos 2 Existencia y unidad de la division euclidiana 3 División de polinomios 3.1 División usual 3.2 División según las potencias crecientes

Ejemplos

El primer ejemplo es detallado - muestra las sustracciones intermediarias - y el segundo sólo muestra los restos.

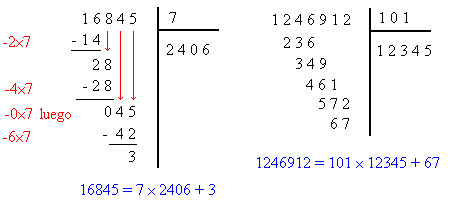
Cuando a o b es negativo, lo más práctico es hacer la división con los valores positivos |a| y |b| y luego adaptar el resultado. A partir del primer ejemplo, se puede hallar las divisiones de (a) 16845 por -7, de (b) -16845 por 7 y de (c) -16845 por -7:
16845 = 7 × 2406 + 3 da:
(a): 16845 = (-7) × (-2406) + 3
-16845 = (-7) × 2406 - 3 lo que no es una división euclidiana porque el resto -3 no es positivo; hay que sumarle 7, que se resta por otra parte:
(b): -16845 = (-7) × 2407 + 4.
Cambiando un signo de lugar en la división anterior se obtiene:
(c): -16845 = 7 × (-2407) + 4

Existencia y unidad de la division euclidiana

e:
Sean a y b positivos, b≠o (los demás casos son muy parecidos). La sucesión (n·b) _{n∈ N} tiende hacia el infinito, por lo tanto dobla a a partir de cierto rango. Sea q el último valor de n tal que n·b sea inferior o igual a a. Entonces, por definición:
q·b ≤ a < (q+1)·b. Al sustraer q·b a todos los miembros, obtenemos:
0≤ a - q·b < b. Llamemos r =a - q·b; entonces a = q·b +r; y la desigualdad anterior se escribe 0≤ r < b.

Unicidad:
Supongamos la existencia de dos escrituras de a: a= bq + r = bq' + r'. Por sustracción:
b·(q - q') = r' - r. Esto implica que b divide r' - r. Pero r y r' pertenecen al intervalo [0; b[ y luego la diferencia pertenece a ]- b; b[. El único elemento de este intervalo divisible por b es cero, por lo tanto r' - r = 0, es decir r = r'. Luego bq + r = bq' + r, lo que se simplifica en q = q'.

Una calculadora facilita la división, si b > 0: 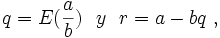donde E es la función parte entera. Esto se obtiene dividiendo la igualdad a = b·q + r por b: 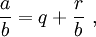y como 0 ≤ r < b, la fracción r/b pertenece a [0; 1[, y es por lo tanto la parte fraccionaria de a, y b es su parte entera.

División de polinomios

División usual

La división euclidiana se generaliza a todos los anillos graduados, es decir en los anillos donde existe una función llamada grado, con valor en {- ∞} ∪ N, notada d ^o, que verifique (entre otras cosas) d ^o(P·Q) = d ^o(P) + d ^o(Q).
Los ejemplos más usuales lo constituyen los anillos de polinomios K[X], donde K es un cuerpo, como R o C, y donde d ^o(Xⁿ) = n y d ^o(0) = - ∞. En este contexto, se remplaza la condición 0≤ r < b que a priori no tiene sentido porque el anillo ya no es totalmente ordenado, por d ^o (R) < d ^o(B), y claro, se mantiene A = B·Q + R (para los polinomios, la costumbre es utilizar las mayúsculas).

La división euclidiana de polinomios permite encontrar el máximo común divisor gracias al algoritmo de Euclides.

Sin embargo, su uso más común es para hallar las raíces de un polinomio dado. En tal caso, el resto tiene que ser nulo, y la división euclidiana es una división en el sentido usual: A = B·Q equivale a Q = A/B, que permite factorizar con rapidez. La resolución de una ecuación de tercer grado requiere mucho tiempo si se aplica el método general. Lo mejor es tratar de encontrar una raíz evidente α y luego dividir P por X - α.

Ejemplo: Sea P = 63X³ - 86X² + 3X + 20 un polinomio de grado 3, y se quiere hallar todas sus raíces. Miremos primero si 0, 1 o -1 es raíz evidente. Por suerte (...) P(1) = 63 - 86 + 3 + 20 = 0. Como x_o = 1 es raíz, podemos factorizar por X - 1, lo que hacemos mediante una división euclidiana:

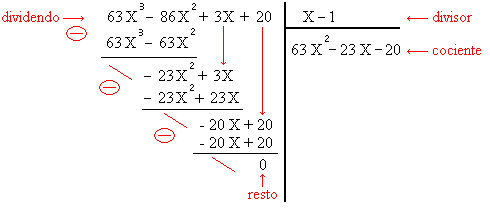
El resto es nulo, lo que confirma que 1 es raíz, y tenemos: P = (X-1)·Q, con Q = 63X² - 23X - 20. Luego, las raíces de Q se obtienen resolviendo la ecuación de segundo grado Q(x) = 0 y se obtiene 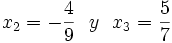y por último se puede completar (y arreglar) la factorización de P: P = (X-1)(7X - 5)(9X + 4).

Si A es un anillo, la división euclidiana en A[X] no es siempre posible. Por ejemplo, en Z[X], los polinomios con coeficientes enteros, no es posible dividir X² por 2X + 3, porque el cociente (trabajando en R[X]) es: X/2, y no pertenece a Z[X].

La única condición para que sea posible es que coeficiente dominante (el del monomio de mayor grado) sea inversible. En el ejemplo detallado, la división por X - 1 ( = 1X - 1) no causó problema alguno porque el coeficiente dominante es 1, inversible en Z.

División según las potencias crecientes

En algunos casos es interesante considerar que X es pequeño frente a 1 y hacer las divisiones al revés, empezando por las constantes (que son los términos mayores) y terminando por los Xⁿ, con n grande. Formalmente, se modifica la definición del grado: d ^o (Xⁿ) = - n. La diferencia es que ya no hay unicidad, y es necesario fijarse por antelación una precisión, es decir un grado máximo al resto.

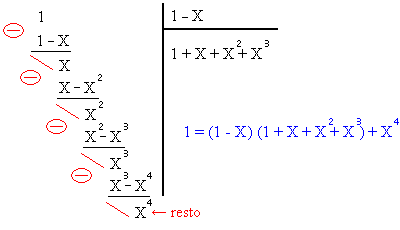
Por ejemplo, dividamos 1 por 1 - X al orden 3: el resto deber haber como término más fuerte (aquí el monomio de menor exponente) a lo mejor X⁴. La igualdad obtenida (en azul) equivale a:

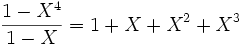
lo que, además de ser cierta, es un caso especial de la suma de términos de una sucesión geométrica:

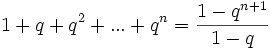
y cada valor de n corresponde a una división euclidiana con una precisión distinta.

Otro punto de vista es considerar a 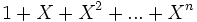como el inicio del desarrollo de 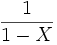en serie de Taylor.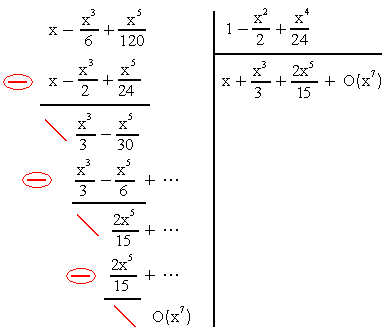

Más generalmente, la serie de Taylor de una función racional se obtiene mediante la división euclidiana de la serie de Taylor del numerador por la del denominador. Por ejemplo, consideremos la función trigonométrica tangente: 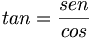, y busquemos su desarrollo alrededor de 0 al orden 5. Hay que conocer las series al orden 5 (por lo menos) del seno y del coseno, y dividirlas descartando sistemáticamente los términos de orden mayor que aparecen en el cálculo. Como la función tangente es par, sólo hay tres monomios (en X, X³ y X⁵) que buscar. El resultado es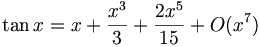

La división euclidiana también existe en los anillos de polinomios de múltiples variable K[X,Y,Z...], donde hay varias maneras de definir el grado (parcial, total...) y otras tantas de proceder a la división.

La primera versión de este artículo porviene de Enciclopedia Libre - División euclidiana publicado bajo la licencia GFDL