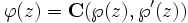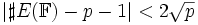En matemáticas, las curvas elípticas se definen mediante ecuaciones cúbicas (de tercer grado). Han sido usadas para probar el último teorema de Fermat y se emplean también en criptografía (para más detalles ver el artículo criptografía de curvas elípticas) y en factorización de enteros. Estas curvas no son elipses.

Las curvas elípticas son "regulares", es decir, no tienen "vértices" ni autointersecciones, y se puede definir una operación binaria para el conjunto de sus puntos de una manera geométrica natural, lo que hace de dicho conjunto un grupo abeliano.

Las curvas elípticas sobre el cuerpo de los números reales vienen dadas por las ecuaciones y² = x³ − x y por y² = x³ − x + 1.

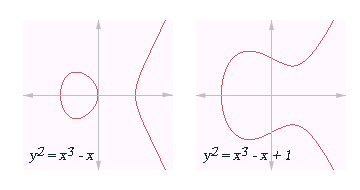
Las curvas elípticas pueden definirse sobre cualquier cuerpo K; la definición formal de una curva elíptica es la de una curva algebraica proyectiva no singular sobre K de género 1.

Si la característica de K no es ni 2 ni 3, entonces toda curva elíptica sobre K puede escribirse en la forma :y² = x³ − px − q donde p y q son elementos de K tales que el polinomio del miembro derecho x³ − px − q no tenga ninguna raíz doble. Si la característica es 2 o 3 harán falta más términos.

Normalmente se define la curva como el conjunto de todos los puntos (x,y) que satisfacen la ecuación anterior, y tales que x e y sean elementos de la cerradura algebraica de K. Los puntos de la curva cuyas coordenadas pertenezcan ambas a K se llaman puntos K-racionales.

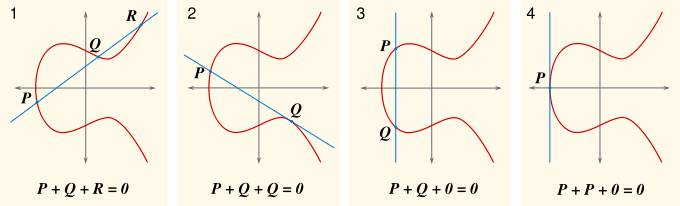
Si añadimos un punto en el "infinito", obtenemos la versión proyectiva de tal curva. Si tenemos dos puntos de la curva, P y Q entonces podemos describir de forma unívoca un tercer punto que sea la intersección de la curva con la línea que contiene los dos puntos P y Q. Si la línea es tangente a la curva en un punto, entonces, ese punto la contará dos veces; y si la línea es paralela al eje y, definimos el tercer punto como en el infinito. Entonces una de tales condiciones será la que cumpla cualquier par de puntos de una curva elíptica.

subgrupo de este grupo. Si la curva se denota por E, este subgrupo se denota a menudo como E(K).

El grupo de arriba se puede describir geométrica y algebraicamente. Dada la curva y² = x³ - px - q sobre el cuerpo K (cuya característica asumimos que no es ni 2 ni 3), y los puntos P = (x_P, y_P) (subíndice P) y Q = (x_Q, y_Q) en la curva, asumimos primero que x_P ≠ x_Q. Sea s = (y_P - y_Q)/(x_P - x_Q); ya que K es un cuerpo, s está bien definido. Entonces podemos definir R = P + Q = (x_R, y_R) mediante

x_R = s² − x_P − x_Q

y_R = − y_P + s(x_P − x_R)

Si x_P = x_Q, entonces hay dos opciones: si y_P = -y_Q, entonces la suma se define como 0; así que el inverso de cada punto de la curva se encuentra reflejándolo en el eje x. Si y_P = y_Q ≠ 0, entonces R = P + P = 2P = (x_R, y_R) vendrá dado por

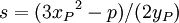
x_R = s² − 2x_P

y_R = − y_P + s(x_P − x_R)

Si y_P = y_Q = 0, entonces P + P = 0.

El teorema de Mordell-Weil establece que si el cuerpo subyacente K es el de los racionales (o más en general un cuerpo numérico), entonces el grupo de puntos K-racionales será finitamente generado. Mientras que se puede determinar fácilmente el subgrupo de torsión de E(K), no se conoce un algoritmo general para computar su rango. Una fórmula para dicho rango viene dada por la conjetura de Birch y Swinnerton-Dyer.

La prueba reciente del último teorema de Fermat se lleva a cabo probando un caso especial de la profunda conjetura de Taniyama-Shimura que relaciona las curvas elípticas sobre los racionales con las formas modulares; dicha conjetura ha sido también completamente demostrada.

Si el cuerpo subyacente K es el de los complejos, toda curva elíptica podrá ser parametrizada por cierta función elíptica y su derivada. Específicamente, a cada curva elíptica E se le asocia un reticulado L y una función elíptica de Weierstrass correspondiente 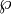, tal que la aplicación

φ : C/L → E

con

sea un isomorfismo de grupos y un isomorfismo de superficies de Riemann. Lo que prueba en particular que topológicamente, E semeja un toro (ya que C/L es un toro). Si el reticulado L está relacionado con otro reticulado cL mediante la multiplicación por un número complejo distinto de cero c, entonces las curvas correspondientes son isomorfas. Las clases de isomorfismo de curvas elípticas se especifican mediante el j-invariante.

Mientras que el número de puntos racionales de una curva elíptica E sobre un cuerpo finito F_p es difícil de computar en general, un teorema de Hasse dice que

Este hecho puede entenderse y demostrarse con algo de teoría general; ver función zeta local, cohomología étale.

Para desarrollos ulteriores ver aritmética de variedades abelianas.

Las curvas elípticas sobre cuerpos finitos se usan en algunas aplicaciones en criptografía así como en la factorización de enteros. La idea general en esas aplicaciones es que si tenemos un algoritmo que usa ciertos grupos finitos podemos reescribirlo usando los grupos de puntos racionales de curvas elípticas.

Véase también

• criptografía de curvas elípticas
• curva elíptica DSA
• factorización Lenstra de curvas elípticas.

Enlaces externos

• Wikimedia Commons alberga contenido multimedia sobre Curva elíptica.Commons
• The Mathematical Atlas: 14H52 Elliptic Curves