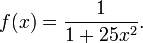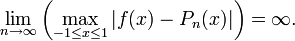Fenómeno de Runge

Fenómeno de Runge

Fenómeno de Runge

La curva roja es la función de Runge, la azul es un polinomio de 5º grado, y la verde es uno de 9º grado. La aproximación sólo empeora

En el campo matemática del análisis numérico, el fenómeno de Runge es un problema que sucede cuando se usa interpolación polinómica con polinomios de alto grado. Lo descubrió Carle David Tolmé Runge cuando exploraba el comportamiento de los errores al usar interpolación polinómica para aproximar determinadas funciones.

Problema

Considérese la función:

f(x) = \frac{1}{1+25x^2}.\,

Runge descubrió que si se interpola esta función en puntos equidistantes xi entre −1 y 1 tal que:

x_i = -1 + (i-1)\frac{2}{n},\qquad i \in \left\{ 1, 2, \dots, n+1 \right\}

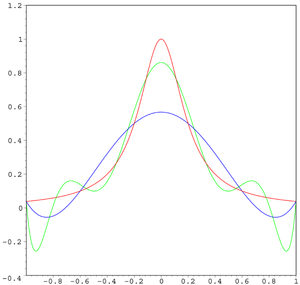
con un polinomio Pn(x) de grado 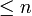\leq n, la interpolación resultante oscila hacia los extremos del intervalo, es decir, cerca de −1 y 1. Incluso se puede probar que el error de interpolación tiende a infinito cuando crece el grado del polinomio:

\lim_{n \rightarrow \infty} \left( \max_{-1 \leq x \leq 1} | f(x) -P_n(x)| \right) = \infty.

Soluciones al problema del fenómeno de Runge

La oscilación se puede minimizar usando nodos de Chebyshev en lugar de equidistantes. En este caso se garantiza que el error máximo disminuye al crecer el orden polinómico. El fenómeno demuestra que los polinomios de grado alto no son, en general, aptos para la interpolación. Este problema se puede evitar usando curvas spline, que son polinomios por partes. Cuando se intenta reducir el error de interpolación se puede incrementar el número de partes del polinomio que se usan para construir el spline, en lugar de incrementar su grado.

Véase también

Obtenido de "Fen%C3%B3meno de Runge"

Wikimedia foundation. 2010.

Игры ⚽ Поможем сделать НИР

Mira otros diccionarios:

  • Carle David Tolmé Runge — Saltar a navegación, búsqueda Carle David Tolmé Runge Carle David Tolmé Runge (30 de agosto de 1856 – 3 de enero de 1927) fue un matemático, físico y espectroscopista alemán. Su primer nombre suele escr …   Wikipedia Español

  • Interpolación polinómica — En análisis numérico, la interpolación polinómica es una técnica de interpolación de un conjunto de datos o de una función por un polinomio. Es decir, dado cierto número de puntos obtenidos por muestreo o a partir de un experimento se pretende… …   Wikipedia Español

  • Polinomio de Chebyshov — Saltar a navegación, búsqueda En matemática, los polinomios de Chebyshov, nombrados en honor a Pafnuti Chebyshov, son una familia de polinomios ortogonales que están relacionados con la fórmula de De Moivre y son definidos de forma recursiva con… …   Wikipedia Español

  • Polinomios de Chebyshov — En matemática, los polinomios de Chebyshov, nombrados en honor a Pafnuti Chebyshov, son una familia de polinomios ortogonales que están relacionados con la fórmula de De Moivre y son definidos de forma recursiva con facilidad, tal como ocurre con …   Wikipedia Español

  • São Paulo — Para otros usos de este término, véase São Paulo (desambiguación). São Paulo …   Wikipedia Español

  • Arte de paisajes — Saltar a navegación, búsqueda Zhan Ziqian, Paseando en Primavera, c. 600 …   Wikipedia Español

  • Historia del arte — Para la historiografía de la historia del arte, véase Estudio de la historia del arte. La creación …   Wikipedia Español

  • Análisis numérico — El análisis numérico o cálculo numérico es la rama de las matemáticas que se encarga de diseñar algoritmos para, a través de números y reglas matemáticas simples, simular procesos matemáticos más complejos aplicados a procesos del mundo real. El… …   Wikipedia Español

  • B-spline — Saltar a navegación, búsqueda En el subcampo matemático de análisis numérico, una B spline es una función spline que tiene el mínimo apoyo con respecto a un determinado grado, suavidad, y partición del dominio. Un teorema fundamental establece… …   Wikipedia Español

  • Virus — Para otros usos de este término, véase Virus (desambiguación) …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”