- Grafo cúbico
-
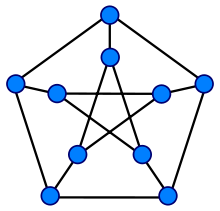El Grafo de Petersen es un grafo cúbico.
En teoría de grafos, un grafo cúbico o grafo trivalente es un grafo cuyos vértices son todos incidentes a exactamente tres aristas. En otras palabras, un grafo cúbico es un grafo 3-regular.
Un grafo bicúbico es un grafo bipartito cúbico.
Contenido
Historia
- 1880: Peter Guthrie Tait conjetura que cada grafo bridgeless cúbico planar tiene un circuito hamiltoniano. William Thomas Tutte encuentra un contra-ejemplo: un grafo de 46 vértices (ahora llamado como él) en 1946.
- 1934: Ronald M. Foster comienza a coleccionar ejemplos de grafos simétricos cúbicos, con lo que se daría inicio al Censo de Foster.[1]
- 1971: William Tutte conjetura que todos los grafos bicúbicos son ciclos hamiltonianos. Sin embargo, Horton proporciona un grafo de contra-ejemplo, con 96-vértices.
- 2003: Petr Hliněný demuestra que el problema de encontrar el número de cruzamiento (el mínimo número de aristas que se cruzan en un grafo dado) de un grafo cúbico es NP-hard, a pesar de que tienen un grado pequeño. Existen, no obstante, algoritmos de aproximación prácticos para encontrar el número de cruzamiento de grafos cúbicos.
Véase también
Referencias
- Weisstein, Eric W., et al. "Tait's Hamiltonian Graph Conjecture". Consultado el 23 de abril de 2005.
- Weisstein, Eric W., et al. "Bicubic graphs". Consultado el 23 de abril de 2005.
- Petr Hliněný. Crossing Number Is Hard for Cubic Graphs. MFCS 2004: 772-782. 2003.
Notas
Categoría:- Familias de grafos
Wikimedia foundation. 2010.
