Grado (teoría de grafos)

Grado (teoría de grafos)
Para otros usos de este término, véase Grado.
Un grafo con vértices etiquetados según su grado. El vértice aislado se etiqueta con 0, pues su grado es igual a cero.

En Teoría de grafos, el grado o valencia de un vértice es el número de aristas incidentes al vértice. El grado de un vértice x es denotado por grado(x), g(x) o gr(x) (aunque también se usa δ(x), y del inglés d(x) y deg(x)). El grado máximo de un grafo G es denotado por Δ(G) y el grado mínimo de un grafo G es denotado por δ(G).

Contenido

Vecindad de un vértice

Artículo principal: Entorno (topología)

Otra forma de definir el grado de un vértice es a través de su vecindad. La vecindad de un vértice x , denotado como N(x)\, está dado por todos los vértices adyacentes a x.

N(x)= \{ y \in V_G | \{ x,y\} \in E_G\}

de modo que el grado del vértice x es el número de vecinos que tiene: g(x)=|N(x)| \,.

Lema del apretón de manos

La fórmula de la sumatoria de grados, que relaciona la valencia de los vértices con el número de aristas es conocida como Lema del apretón de manos:

Lema del apretón de manos. La suma de los grados de un grafo G(V,E)\, es igual al doble del número de aristas:

\sum_{v \in V} g(v) = 2|E|\,

Euler[1] (1736)

Su demostración es una prueba del doble conteo, esto porque, como cada arista tiene dos vértices extremos, es contada dos veces en las valencias de estos.

Algunas implicaciones del Lema del apretón de manos son:

  • En un grafo siempre hay un número par de valencias de grado impar.
  • No puede existir un grafo r-regular de s vertices si r y s son impares.
  • El número de aristas de un grafo k-regular es a=\frac{k(k-1)}{2}, y por ende, el número de aristas de un grafo completo de n vertices es a=\frac{n(n-1)}{2}

Digrafos

En el caso de los dígrafos, se suele distinguir entre valencia de entrada g^{+} (x)\, , como el número de aristas que tiene al vértice x como vértice final y la valencia de salida g^{-} (x)\, como el número de aristas que tiene al vértice x como vértice inicial, de forma que g(x)= g^{+} (x)+ g^{-} (x)\, .


El Lema del apretón de manos también es cierto en los dígrafos, para ello hay que distinguir entre valencia de entrada y la valencia de salida de algún vértice x. Por lo tanto, el Lema se expresa del siguiente modo:

\sum_{v \in V} g^{+}(v)= \sum_{v \in V} g^{-}(v) = |E|\,

Secuencia de grados

Artículo principal: Secuencia de grados

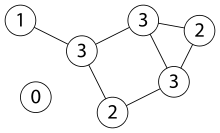
Una secuencia de grados o lista de grados de un grafo no-dirigido es una secuencia de números, los cuales son grados de los vértices de algún grafo. Para el grafo de la imagen su secuencia de enteros es (3, 3, 3, 2, 2, 1, 0). La lista de grados es un invariante (topológica) de un grafo, aunque dos grafos con igual lista de grados no son necesariamente isomorfos.

Un problema interesante es determinar si una secuencia de enteros no-negativos cualquiera es o no gráfica, es decir, es una secuencia de grados de un grafo (simple). Erdős y Gallai[2] (1960) resuelven el problema con su teorema de existencia, mientras que Havel[3] (1955) y Hakimi[4] (1962) nos entregan un teorema de construcción que justifica el Algoritmo Havel-Hakimi para construir un grafo a partir de una secuencia de grados.

Teorema de Erdős-Callai. La secuencia de enteros d_i \, con i=1,...,n-1 \, es una secuencia de grados de un grafo simple, si y sólo si:

  • La suma de los enteros de la secuencia es par, y
  • \sum_{i=1}^{k}d_i \leq k(k-1) + \sum_{i=k+1}^n \min(d_i,k)

Teorema de Havel-Hakimi. Una secuencia de enteros d_1 \geq d_2 \geq ... \geq d_v \geq 0 es gráfica sí, y sólo sí también lo es la lista: d_{2}-1, d_{3}-1, ..., d_{d_{1}+1}-1, d_{d_{1}+2}, ... , d_v, que resulta de eliminar el primer elemento y restar una unidad a los siguientes d1 valores de la lista.

Valores especiales

  • Un vértice con grado 0 se llama vértice aislado. Un grafo formado por vértices aislados se llama grafo vacio
  • En un árbol, el vértice de grado 1 se llama hoja y forma parte del grupo de los vértices terminales.

Propiedades globales

  • Si cada vértice de un grafo cualquiera tiene grado k, entonces el grafo es llamado grafo regular de grado k.
  • Un grafo simple conexo contiene un camino Euleriano sí, y sólo sí el grafo contiene 0 ó 2 vértices de grado impar. Si el grafo no tiene vértices de grado impar entonces contiene un ciclo Euleriano.
  • Por el Teorema de Brooks el número cromático de un grafo G que no es un grafo completo ni un ciclo de longitud impar es a lo sumo: \chi (G)\leq \Delta , y por el Teorema de Vizing todo grafo tiene índice cromático a lo más Δ + 1

Véase también

Referencias

  1. ↑ Euler, L. (1736). «Solutio problematis ad geometriam situs pertinentis». Commentarii Academiae Scientiarum Imperialis Petropolitanae 8. 128-140. http://math.dartmouth.edu/~euler/docs/originals/E053.pdf. 
  2. ↑ Erdős, P. ; Gallai, T. (1960). «Graphs with prescribed degree of vertices». Mat. Lapok 11. 264–274.. 
  3. ↑ Havel, V. (1955). «A remark on the existence of finite graphs.». Časopis Pest. Mat. 80. 477–480.. 
  4. ↑ Hakimi, S.L. (1962). «On the realizability of a set of integers as degrees of the vertices of a simple graph». J. SIAM Appl. Math 10. 496–506.. 

Wikimedia foundation. 2010.

Игры ⚽ Нужен реферат?

Mira otros diccionarios:

  • Vértice (teoría de grafos) — Para otros usos de este término, véase vértice. Un grafo con 6 vértices y 7 aristas. En teoría de grafos, un vértice o nodo es la unidad fundamental de la que están formados los grafos. Un grafo no dirigido está formado por un conjunto de… …   Wikipedia Español

  • Teoría de grafos — Diagrama de un grafo con 6 vértices y 7 aristas. En matemáticas y en ciencias de la computación, la teoría de grafos (también llamada teoría de las gráficas) estudia las propiedades de los grafos (también llamadas gráficas). Un grafo es un… …   Wikipedia Español

  • Bucle (teoría de grafos) — Un grafo con un bucle en el vértice 1. En teoría de grafos, un bucle o loop es una arista que conecta un vértice consigo mismo. Un grafo simple no posee bucles. Dependiendo del contexto, un grafo o multigrafo puede estar definido o no para… …   Wikipedia Español

  • Árbol (teoría de grafos) — Para otros usos de este término, véase Árbol (desambiguación). Árbol Árbol etiquetado con 6 vértices y 5 aristas. El único camino simple que conecta los vértices 2 y 6 es 2 4 5 6 …   Wikipedia Español

  • Estrella (teoría de grafos) — Estrella S7. En teoría de grafos, una estrella Sk es el grafo bipartito completo K1,k, un árbol con un vértice interno y k hojas. Una estrella con 3 aristas se conoce en inglés como claw (garra o garfio). La estrella Sk es tran …   Wikipedia Español

  • Glosario en teoría de grafos — Anexo:Glosario en teoría de grafos Saltar a navegación, búsqueda Grafo con 6 nodos A continuación se detallan los principales conceptos de la teoría de grafos. Para las definiciones formales o más detalladas, puede dirigirse al artículo principal …   Wikipedia Español

  • Anexo:Glosario de teoría de grafos — Grafo simple no dirigido, con 6 vértices y 7 aristas. A continuación se detallan los principales conceptos de la teoría de grafos. Para las definiciones formales o más detalladas, puede dirigirse al artículo principal correspondiente. Todos los… …   Wikipedia Español

  • Grado (matemática) — Este ártículo trata del grado tal y como es empleado en el área de las matemáticas. Para significados alternativos de esta palabra, véase grado. En matemáticas existen diferentes significados de la palabra grado dependiendo del área matemática de …   Wikipedia Español

  • Teoría de Matrices — Saltar a navegación, búsqueda La teoría de matrices es un rama de las matemáticas que se centra en el estudio de matrices. Inicialmente una rama secundaria del álgebra lineal, ha venido cubriendo los temas relacionados con la teoría de grafos, el …   Wikipedia Español

  • Grado — puede referirse a: el grado de comparación o significación de un adjetivo; el grado como distinción académica en educación; el grado en matemática, además de nombrar a distintas unidades de medida de ángulos nombra: el grado de un polinomio, y… …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”