Homeomorfismo de grafos

Este término no debe confundirse con isomorfismo de grafos.

En Teoría de grafos, decimos que dos grafos G₁ y G₂ son homeomorfos si ambos pueden obtenerse a partir de un mismo grafo por una sucesión de subdivisiones elementales de aristas. Suele notarse por .

Este concepto, de naturaleza combinatoria, está relacionado con el concepto topológico de homemorfismo: cualquier grafo puede representarse como un espacio topológico en que cada vértice queda representado por un punto distinto y cada arista por un arco homeomorfo con el intervalo [0,1]. Dos grafos son homeomorfos en el sentido de la teoría de grafos si y solo si lo son como espacios topológicos.

Ejemplo

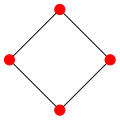
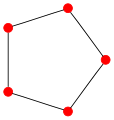
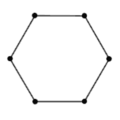
Todos los grafos ciclo de n vértices son homeomorfos entre sí. Por ejemplo, si se hace una subdivisión elemental de algún vértice de C₄ se obtiene un C₅. Finalmente, si al C₅ se le aplica nuevamente una subdivisión elemental se logra el C₆. Como tanto C₅ y C₆ se obtuvieron de C₄ se dice que C₅ es homeomorfo a C₆ y se nota

• 

  C₄

• 

  C₅

• 

  C₆