- Isomorfismo de grafos
-
En teoría de grafos, un isomorfismo entre dos grafos G y H es una biyección f entre los conjuntos de sus vértices
que preserva la relación de adyacencia. Es decir, cualquier par de vértices u y v de G son adyacentes si y solo si lo son sus imágenes, f(u) y f(v), en H.A pesar de su diferente aspecto, los dos grafos que se muestran a continuación son isomorfos:
Grafo G Grafo H Un isomorfismo
entre G y H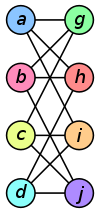
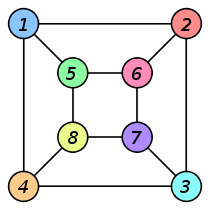
f(a) = 1 f(b) = 6
f(c) = 8
f(d) = 3
f(g) = 5
f(h) = 2
f(i) = 4
f(j) = 7
Dos grafos con matrices de adyacencia respectivas A y B serán isomofos si y solo si existe una matriz permutación P tal que B = P A Pt.[1]
Problema del isomorfismo de grafos
La determinación de si dos grafos con el mismo número de vértices n y aristas m son isomorfos o no se conoce como el problema del isomorfismo de grafos. Este problema admite un ataque por fuerza bruta que exigiría comprobar si las n! biyecciones posibles preservan la adyacencia, pero no se conoce un algoritmo eficiente, al menos para el caso general. En este contexto, eficiencia debe interpretarse como crecimiento del número de pasos inferior a O(en).
El problema del isomorfismo de grafos presenta una curiosidad en teoría de complejidad computacional al ser uno de los pocos problemas citados por Garey y Johnson en 1979 pertenecientes a NP de los que se desconoce si es resoluble en tiempo polinómico o si es NP-completo (actualmente está en revisión la demostración de que el problema está en P).[2]
Referencias
Wikimedia foundation. 2010.
