- Homología (geometría)
-
En geometría, una homología es una transformación homográfica resultante de efectuar una proyección desde un punto, en la que a cada uno de los puntos y las rectas de una figura plana le corresponden, respectivamente, un punto y una recta de su figura homológica, cumpliendose por tanto que:
- Un punto P y su imagen P' siempre están alineados con un punto llamado centro de la homología (O). El centro de homología es invariante.
- La imagen de una recta R es otra recta R'.
- Una recta R y su imagen R' siempre se cortan sobre una recta llamada eje de homología (e). Cada punto sobre esta recta es invariante. Se denomina a ese punto punto doble de la recta R.
- La incidencia se preserva. Por ejemplo si dos rectas R y S se cortan en un punto P, sus imágenes R' y S' se cortarán en la imagen del punto P P'.
Determinación imágenes de puntos en un sistema de homología
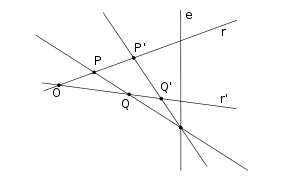
Para determinar la imagen Q' de un punto Q del plano, nos bastaremos de ese par de puntos P y P' que tenemos originalmente. Trazamos una recta PQ, que tendrá un punto doble sobre el eje de homología. La imagen de esa recta PQ tendrá que pasar forzosamente por ese punto doble y por P'. Sobre la imagen de PQ tendrá que estar Q'. También tendrá que estar Q' sobre la recta que une el centro de homología O y Q. Interseccionando PQ' y OQ lograremos la imagen Q' buscada. Para hallar la imagen I' de un punto I en el infinito (punto virtual o impropio), se procede de manera semejante. Se traza la recta PI (que será una dirección), que corta al eje de homología (e) en un punto doble Q. Dicha recta se transforma en la recta P'Q. La imagen del punto I, como cualquier otro punto, se halla sobre la intersección de la recta P'Q con la recta OI (en el plano euclídeo, las rectas PI y IOI' son paralelas). Se verifica que la recta L, paralela al eje de homología e por el punto I', el lugar geométrico de todas las imágenes de los puntos impropios del plano, y recibe la denominación de recta límite.
Véase también
- Homografía
- Afinidad
Categorías:- Geometría proyectiva
- Transformaciones geométricas
Wikimedia foundation. 2010.
