Ley de la inversa del cuadrado

Ley de la inversa del cuadrado
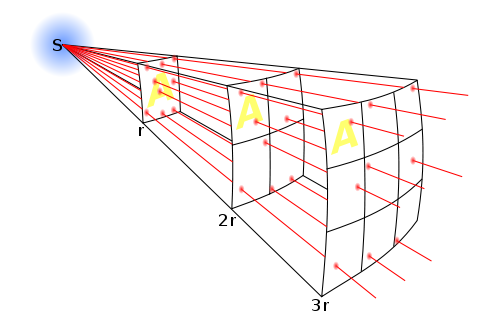Ilustración de la ley de la inversa del cuadrado. Las líneas representan el flujo que emana de una fuente puntual. La densidad de líneas de flujo disminuye a medida que aumenta la distancia.

La ley de la inversa del cuadrado o ley cuadrática inversa refiere a algunos fenómenos físicos cuya intensidad disminuye con el cuadrado de la distancia al centro donde se originan. En particular, se refiere a fenómenos ondulatorios (sonido y luz) y campos centrales.

Contenido

Discusión

En mecánica ondulatoria la ley de la inversa del cuadrado establece que para una onda como, por ejemplo, el sonido o la luz, que se propaga desde una fuente puntual en todas direcciones por igual, la intensidad de la misma disminuye de acuerdo con el cuadrado de la distancia a la fuente de emisión. Esta ley se aplica naturalmente a la intensidad sonora y a la intensidad de luz (iluminación), puesto que tanto el sonido como la luz son fenómenos ondulatorios. A distancias suficientemente grandes de los emisores de luz o sonido, estos pueden ser vistos como fuentes puntuales. Por ejemplo, si se considera una fuente de luz pequeña y se hacen mediciones de la intensidad lumínica a una distancia d y a una distancia 2d, en el primer caso la intensidad es [(1/d)/(1/2d)]² = 4 veces mayor que en el segundo.

En teoría clásica de campos, en particular en campos centrales, la intensidad de campo también está gobernada por una ley de la inversa del cuadrado. Típicamente se observa en:

El hecho de que los campos centrales disminuyan de intensidad según la inversa del cuadrado, está relacionado con que el espacio tiene tres dimensiones espaciales. De hecho, puede probarse que todo campo central que responde a la ecuación de Poisson en un espacio de D dimensiones decrece a grandes distancias como 1/rD-1, siendo r la distancia al centro de la fuente del campo.

Deducción de la ley inversa para ondas

La ley de la inversa del cuadrado para la intensidad de una onda sonora lumínica o de otro tipo puede ser deducida rigurosamente a partir de la ecuación de onda (1) y la definición de intensidad (2), tal como sigue. Se parte de las siguientes ecuaciones:

(1) \nabla^2 \Psi -\frac{1}{c^2}\frac{\partial^2 \Psi}{\partial t^2} = 0

(2) I = <\Psi^2(r,t)>_t \,

Para una onda esférica emitida por una fuente puntual, Ψ sólo depende de la distancia r al centro de emisión y por tanto escribiendo el operador laplaciano que aparece en la ecuación de onda (1) en coordenadas esféricas para Ψ = Ψ(r,t) se tiene:

(1') \frac{1}{r^2} \frac{\partial}{\partial r}\left( r^2\frac{\partial \Psi}{\partial r} \right)-\frac{1}{c^2}\frac{\partial^2 \Psi}{\partial t^2} = 0

La solución de la ecuación de onda anterior, con c = ω/k, es:

\Psi(r) = \frac{A_0}{r} \cdot sin(\omega t - kr + \alpha)

Se puede aplicar la ecuación (1) para la intensidad o promedio cuadrático temporal <Ψ2>t es igual a:

I = \frac{A_0^2}{r^2}

Es decir, este último resultado muestra que la intensidad decrece con el cuadrado de la distancia al centro emisor, que es lo que se pretendía probar.

Deducción de la ley inversa para campos centrales

Si V(r) es un campo central y, por tanto, con simetría esférica, generado por una densidad de carga ρ o de masa concentrada y que satisface la ecuación de Laplace (3), entonces el campo para distancias grandes de la fuente viene dado por la ecuación:

(3) \nabla^2 V(r) = 0

Que escribiendo en coordenadas esféricas el operador laplaciano para un espacio de D dimensiones nos lleva a:

(3') \frac{1}{r^{D-1}} \frac{\partial}{\partial r}\left( r^{D-1}\frac{\partial V(r)}{\partial r} \right) = 0

La solución de esa ecuación se puede calcular muy fácilmente y es precisamente:

(4) V(r) = \frac{k_c p}{r^{D-2}}

Donde kc es la constante del campo, p el valor total de la fuente (masa o carga total de la fuente que crea el campo) y D el número de dimensiones del espacio. Para un espacio tridimensional D = 3, el campo de fuerzas descrito por (3) viene dado por:

(5) \mathbf{F}(r)= \mathbf{\nabla}V(r) = \frac{k_c p}{r^{2}} \mathbf{\hat r} \qquad \mbox{con} \qquad p = \frac{1}{k_c} \int_{Vol(r)} \rho \quad dV

Es decir, un campo con simetría esférica descrito por el potencial (3) en un espacio de tres dimensiones debe decrecer según la ley inversa del cuadrado.

Véase también


Wikimedia foundation. 2010.

Игры ⚽ Нужна курсовая?

Mira otros diccionarios:

  • Ley de la inversa del cuadrado — En física existen varias leyes que también reciben este nombre, por que en su formulación aparece esta expresión inversa del cuadrado de la distancia . Se trata de fenómenos que tienen una variación que se puede representar con una ecuación… …   Enciclopedia Universal

  • Ley de Coulomb — expresando los signos de cargas de diferente signo, y de carga del mismo signo. La ley de Coulomb puede expresarse como: La magnitud de cada una de las fuerzas eléctricas con que interactúan dos cargas puntuales en reposo es directamente… …   Wikipedia Español

  • Ley de gravitación universal — Fuerzas mutua de atracción entre dos esferas de diferente tamaño. De acuerdo con la mecánica newtoniana las dos fuerzas son iguales en módulo y dirección, pero contrarias en sentido; al estar aplicadas en diferentes cuerpos no se anulan y su… …   Wikipedia Español

  • Ley cuadrática inversa (sonido) — En sonido, la ley de la inversa del cuadrado establece que la intensidad de sonido de un frente de onda disminuye, conforme este frente de ondas se aleja de la fuente sonora que lo ha originado, de manera inversamente proporcional al cuadrado de… …   Enciclopedia Universal

  • Ley cuadrática inversa (luz) — La ley de la inversa del cuadrado o ley cuadrática inversa establece que la zona iluminada por una fuente puntual de luz, disminuye si esa mima fuente es colocada al doble de distancia. Entonces, la zona ilumniada pasa a ser veces menor. En… …   Enciclopedia Universal

  • Ley de Beer-Lambert — En óptica, la ley de Beer Lambert, también conocida como ley de Beer o ley de Beer Lambert Bouguer es una relación empírica que relaciona la absorción de luz con las propiedades del material atravesado. Contenido 1 Expresión 2 Ley de Beer Lambert …   Wikipedia Español

  • Teoría de la gravitación de Le Sage — La Teoría de la gravitación de Le Sage, referida también con el nombre de teoría cinética de la gravitación fue concebida originariamente por Nicolas Fatio de Duillier en 1690 y desarrollada ulteriormente por Georges Louis Le Sage en 1748. La… …   Wikipedia Español

  • Fuerza — Para otros usos de este término, véase Fuerza (desambiguación). Descomposición de las fuerzas que actúan sobre un sólido situado en un plano inclinado. En física, la fuerza es una magnitud física que mide la intensidad del intercambio de momento …   Wikipedia Español

  • Historia del electromagnetismo — La Historia del electromagnetismo, que es el conocimiento y el uso registrado de las fuerzas electromagnéticas, data de hace más de dos mil años. En la antigüedad ya estaban familiarizados con los efectos de la electricidad atmosférica, en… …   Wikipedia Español

  • Onda esférica — La exactitud de la información en este artículo o sección respecto a no hay referencias está discutida. En la página de discusión puedes consultar el debate al respecto. Una onda esférica, en física, es aquella onda tridimensional que se propaga… …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”