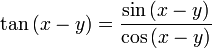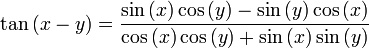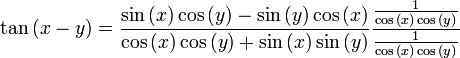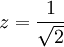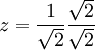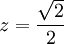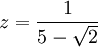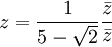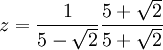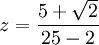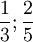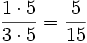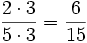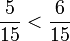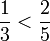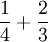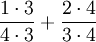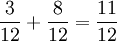Amplificación y simplificación de fracciones

Amplificación y simplificación de fracciones

Amplificación y simplificación de fracciones

En matemática, amplificar una fracción es la acción de multiplicar tanto el numerador como el denominador de ésta, por un mismo número, con el objetivo de obtener una fracción equivalente[1] a la fracción inicial. La simplificación o reducción de fracciones a la acción de dividir numerador y denominador de una fracción por un mismo número con el objetivo de obtener una fracción equivalente.

Contenido

Amplificación de fracciones

El procedimiento es válido para todo número real distinto de cero, ya que, haciendo uso de la propiedad que posee el elemento Neutro multiplicativo[2] del conjunto de Números Reales (Anillo con unidad), se puede tomar una fracción que sea equivalente a 1 (elemento neutro) de tal manera que su numerador y denominador sean números reales iguales no nulos. Lo anterior se escribe como sigue.


Sean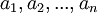 a_1, a_2, ..., a_n \,\! números reales cualesquiera distintos de cero, entonces se tiene que:


\frac{a_1}{a_1}=\frac{a_2}{a_2}=...=\frac{a_n}{a_n}=1 \,\!


No es válida para el real cero porque la división por cero no está definid

Aplicación de fracciones

  • Este procedimiento matemático es usado con frecuencia en muchas demostraciones matemáticas, ya que cualquier expresión que sea multiplicada por 1 no altera su valor. Así entonces, puede crearse una fracción equivalente a uno que nos sea útil en nuestra demostración. Ver ejemplo 1.
(Una función parecida cumple el elemento neutro aditivo de lo números reales, ya que al sumar cero tampoco se altera la expresión).
  • Otro ejemplo muy conocido es el de utilizar esta propiedad en la racionalización de fracciones, donde se usa la propiedad del elemento neutro multiplicativo para sacar[3] la raíz inexacta de un número real del denominador. Ver ejemplo 2.
  • También se usa para comparar fracciones. Acá también es válida la simplificación, que en el fondo es lo mismo, ya que hace uso de las mismas propiedades y procedimientos. Ver ejemplo 3.

Ejemplos de amplificación de fracciones

Ejemplo 1

  • Demostrar que:
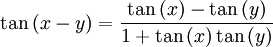\tan {(x-y)} = \frac{\tan {(x)}-\tan {(y)}}{1+\tan {(x)}\tan {(y)}}.

Demostración:

\tan {(x-y)} = \frac{\sin {(x-y)}}{\cos {(x-y)}}
\tan {(x-y)} = \frac{\sin {(x)}\cos {(y)}-\sin {(y)}\cos {(x)}}{\cos {(x)}\cos {(y)}+\sin {(x)}\sin {(y)}}


Multiplicando por 1 el lado derecho de la identidad, tenemos que:

\tan {(x-y)} = \frac{\sin {(x)}\cos {(y)}-\sin {(y)}\cos {(x)}}{\cos {(x)}\cos {(y)}+\sin {(x)}\sin {(y)}}\frac{\frac{1}{\cos {(x)}\cos {(y)}}}{\frac{1}{\cos {(x)}\cos {(y)}}}

Luego,

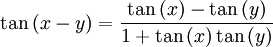\tan {(x-y)} = \frac{\tan {(x)}-\tan {(y)}}{1+\tan {(x)}\tan {(y)}}.

Que es lo que queríamos demostrar.

Nótese que este procedimiento es válido sólo si el producto de las tangentes de x e y son distintos de menos uno.

Ejemplo 2

  • Racionalizar la expresión siguiente:
z = \frac{1}{\sqrt{2}}

Multiplicando por uno tenemos:

z = \frac{1}{\sqrt{2}}\frac{\sqrt{2}}{\sqrt{2}}

Luego,

z = \frac{\sqrt{2}}{2}

O también en el caso siguiente:

  • Racionalizar la expresión:
z = \frac{1}{5-\sqrt{2}}

Multiplicando por el conjugado de z dividido en sí mismo tenemos.

z = \frac{1}{5-\sqrt{2}}\frac{\bar z}{\bar z}
z = \frac{1}{5-\sqrt{2}}\frac{5+\sqrt{2}}{5+\sqrt{2}}
z = \frac{5+\sqrt{2}}{25-2}
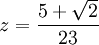z = \frac{5+\sqrt{2}}{23}.


Ejemplo 3

La amplificación puede usarse, entre otras cosas, para saber cuál es la mayor de dos fracciones con diferente denominador (amplificando la fracción de menor denominador hasta dar con una fracción de igual denominador a la otra y comparando después los numeradores).

Si se quiere saber qué fracción es mayor:

\frac{1}{3} ; \frac{2}{5}

Amplificamos la primera por cinco quintos y la segunta por tres tercios:

Esto es,

\frac{1 \cdot 5}{3 \cdot 5} = \frac{5}{15}
\frac{2 \cdot 3}{5 \cdot 3} = \frac{6}{15}

La idea es que ambas tengan el mismo denominador, así, se comparan los numeradores y se decide cuál es mayor.

pudiendo de esta manera comparar las fracciones:

\frac{5}{15} < \frac{6}{15}

y establecer por último la relación:

\frac{1}{3} < \frac{2}{5}


Ejemplo 4

También se usa este procedimiento para sumar fracciones (sumas y restas)

\frac{1}{4} + \frac{2}{3}
\frac{1\cdot 3}{4\cdot 3} + \frac{2\cdot 4}{3\cdot 4}
\frac{3}{12} + \frac{8}{12} = \frac{11}{12}

Simplificación de fracciones

En matemáticas se conoce como simplificación o reducción de fracciones a la acción de dividir numerador y denominador de una fracción por un mismo número con el objetivo de obtener una fracción equivalente.


Ejemplo:

La fracción 2/4 puede simplificarse dividiendo 2:2=1 y 4:2=2, con lo que se obtiene la fracción 1/2 (2/4 = 1/2). Aquella fracción que no puede ser simplificada recibe el nombre de fracción irreducible. Una fracción es irreducible cuando, tanto numerador como denominador son relativamente primos (primos entre sí).se puede dividir por el que se pueda para obtener la fracción correspondiente.

Referencias

  1. ↑ Se llama "fracciones equivalentes" al conjunto de fracciones cuyos cuocientes (o cocientes) tienen el mismo valor numérico. (equi = igual/valente = valor).
  2. ↑ Elemento de un anillo que posee la siguiente propiedad. Si x1 = 1x = x, entonces 1 es el elemento neutro multiplicativo del anillo.
  3. ↑ Se usa esta expresión para referirse a la acción de dejar un número racional por medio de ciertos pasos, en el denominador.
Obtenido de "Amplificaci%C3%B3n y simplificaci%C3%B3n de fracciones"

Wikimedia foundation. 2010.

Игры ⚽ Нужна курсовая?

Mira otros diccionarios:

  • Amplificación y simplificación de radicales — Saltar a navegación, búsqueda Amplificación de radicales Ejemplo: = . Para amplificar un radical, se debe primero transformar éste en una potencia racional, donde el índice de la raíz es el denominador de la fracción y el exponente que eleva a la …   Wikipedia Español

  • Simplificación — Simplificación, simplificar y simplificado puede referirse a: Lo contrario de complicación (complicar, complicado dificultad, difícil ) Lo relativo a la simplicidad (simple facilidad, facilitar, fácil ) Un concepto matemático (véase Amplificación …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”