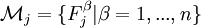En estadística, el análisis de componentes principales (en español ACP, en inglés, PCA) es una técnica utilizada para reducir la dimensionalidad de un conjunto de datos. Intuitivamente la técnica sirve para determinar el número de factores subyacentes explicativos tras un conjunto de datos que expliquen la variabilidad de dichos datos.

Técnicamente, el PCA busca la proyección según la cual los datos queden mejor representados en términos de mínimos cuadrados. PCA se emplea sobre todo en análisis exploratorio de datos y para construir modelos predictivos. PCA comporta el cálculo de la descomposición en autovalores de la matriz de covarianza, normalmente tras centrar los datos en la media de cada atributo.

Contenido 1 Fundamento 2 Matemáticas del ACP 2.1 Método basado en las covarianzas 2.2 Método basado en correlaciones 3 Ejemplos 4 Referencia 4.1 Enlaces externos

Fundamento

El ACP construye una transformación lineal que escoge un nuevo sistema de coordenadas para el conjunto original de datos en el cual la varianza de mayor tamaño del conjunto de datos es capturada en el primer eje (llamado el Primer Componente Principal), la segunda varianza más grande es el segundo eje, y así sucesivamente. Para construir esta transformación lineal debe construirse primero la matriz de covarianza o matriz de coeficientes de correlación. Debido a la simetría de esta matriz existe una base completa de vectores propios de la misma. La transformación que lleva de las antiguas coordenadas a las coordenadas de la nueva base es precisamente la transformación lineal necesaria para reducir la dimensionalidad de datos. Además las coordenadas en la nueva base dan la composición en factores subyacentes de los datos iniciales.

Una de las ventajas de ACP para reducir la dimensionalidad de un grupo de datos, es que retiene aquellas características del conjunto de datos que contribuyen más a su varianza, manteniendo un orden de bajo nivel de los componentes principales e ignorando los de alto nivel. El objetivo es que esos componentes de bajo orden a veces contienen el "más importante" aspecto de esa información.

Matemáticas del ACP

Supongamos que existe una muestra con n individuos para cada uno de los cuales se han medido m variables (aleatorias) 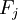. El ACP permite encontrar un número de factores subyacentes p < m que explican aproximadamente el valor de las m variables para cada individuo. El hecho de que existan estos p factores subyacentes puede interpretarse como una reducción de la dimensionalidad de los datos: donde antes necesitabamos m valores para caracterizar a cada individuo ahora nos bastan p valores. Cada uno de los p encontrados se llama componente principal, de ahí el nombre del método.

Existen dos formas básicas de aplicar el ACP:

1. Método basado en la matriz de covarianzas, que se usa cuando los datos son dimensionalmente homogéneos y presentan valores medios similares.
2. Método basado en la matriz de correlación, cuando los datos no son dimensionalmente homogéneos o el orden de magnitud de las variables aleatorias medidas no es el mismo.

Método basado en las covarianzas

Es el más usado cuando todos los datos son homogéneos y tienen las mismas unidades. Cuando se usan valores muy variables o magnitudes que tienen unidades resulta más adecuado para interpretar los resultados el método basado en correlaciones, que siempre es aplicable sin restricción alguna.

Método basado en correlaciones

El método parte de la matriz de correlaciones, consideremos el valor de cada una de las m variables aleatorias 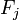. Para cada uno de los n individuos tomemos el valor de estas variables y escribámosla el conjunto de datos en forma de matriz:

.

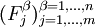Obsérvese que cada conjunto

puede considerarse una muestra aleatoria para la variable 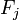. A partir de los mxn datos correspondientes a las m variables aleatorias, puede construirse la matriz de correlación muestral viene definida por:

Puesto que la matriz de correlaciones es simétrica entonces resulta diagonalizable y sus valores propios 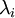verifican: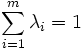

Debido a la propiedad anterior estos m valores propios reciben el nombre de pesos de cada uno de los m componentes principales. Los factores principales identificados matemáticamente se representan por la base de vectores propios de la matriz 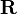. Está claro que cada una de las variables puede ser expresada como combinación lineal de los vectores propios o componentes principales.

Ejemplos

• Una análisis consideró las calificaciones escolares n = 15 estudiantes en m = materias (lengua, matemáticas, física, inglés, filosofía, historia, química, gimnasia). Los dos primeros componentes principales explicaban juntos el 82,1% de la varianza. El primer de ellos parecía fuertemente correlacionado con las materias de humanidades (lengua, inglés, filosofía, historia) mientras que el segundo aparecía relacionado con las materias de ciencias (matemáticas, física, química). Así parece que existe un conjunto de habilidades cognitivas relacionadas con las humanidades y un segundo relacionado con las ciencias, estos dos conjuntos de habilidades son estadísticamente independientes por lo que un alumno puede puntuar alto en sólo uno de ellos, en los dos o en ninguno.^[1]
• Un análisis de metodología docente, consideró las calificaciones de n = 54 estudiantes de la facultad de Biología de la ULA y m = 8 tipos de habilidades. El primer factor principal que explicaba las calificaciones era la inteligencia del estudiante y en segundo lugar la metodología de aprendizaje usada.^[2]
• Una análisis de 11 indicadores socieconómicos de 96 países, reveló que los resultados podían explicarse en alto grado a partir de sólo dos componentes principales, el primero de ellos tenía que ver con el nivel de PIB total del país y el segundo con el índice de ruralidad.^[3]

Referencia

Enlaces externos

• Matemáticas del ACP y ejemplos (Universidad Carlos III de Madrid)