Método de Box-Muller

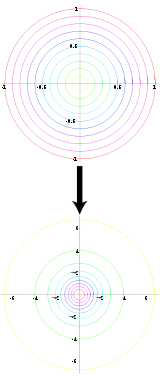Diagrama de la transformada de Box Müller. Los círculos iniciales, se encuentran uniformemente espaciados respecto al origen, están graficados junto con otro conjunto de círculos centrados en el origen donde la separación entre ellos aumenta a medida que se alejan del origen. Los círculos más grandes del dominio se corresponden con los círculos más pequeños en el rango (o codominio) y vice versa.

El método de Box-Muller (nombrado así por sus inventores George Edward Pelham Box y Mervin Edgar Müller 1958)^[1] es un método de generación de pares de números aleatorios independientes con distribución normal "estándar" (esperanza cero y varianza unitaria), a partir de una fuente de números aleatorios uniformemente distribuidos.

Se lo encuentra expresado de dos formas. La forma básica es la que desarrollaron Box y Müller, y toma dos muestras de la distribución uniforme en el intervalo (0, 1] y las transforma en dos muestras con distribución normal. El método polar toma dos muestras de un intervalo distinto, [−1, +1], y las transforma a dos muestras normalmente distribuidas sin utilizar las funciones seno o coseno.

También es posible utilizar el método de la transformada inversa para generar números aleatorios distribuidos normalmente; en comparación el método de Box-Müller posee la ventaja de ser más eficiente desde un punto de vista computacional.^[2] También es posible utilizar el algoritmo Ziggurat que es más eficiente.

Forma básica

Se supone que U₁ y U₂ son variables aleatoria independientes que están uniformemente distribuidas en el intervalo (0, 1]. Sea

y

Entonces Z₀ y Z₁ son variables aleatorias independentes con una distribución normal con desviación típica 1.

La demostración^[3] se basa en el hecho que, en un sistema cartesiano bidimensional donde las coordenadas X e Y son dadas por dos variables aleatorias independientes y distribuidas normalmente, las variables aleatorias para R² y Θ (indicadas previamente) en las coordenadas polares correspondientes también son independientes y poseen las expresiones:

y

Método polar

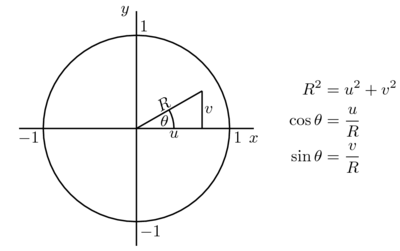Dos valores uniformemente distribuidos, u y v son usados para producir el valor s = R², el cual también se encuentra distribuida en forma uniforme. Las definiciones del seno y del coseno se aplican luego sobre la forma básica de la transformada de Box-Müller Transform de manera de evitar el uso de funciones trigonométricas.

La forma polar Devroye^[4] se la atribuye a Marsaglia. También es mencionada en Carter, aunque sin atribuirla a nadie en particular.^[5]

Dados u y v, independentes y uniformemente distribuidos en un intervalo cerrado [−1, +1], sea s = R² = u² + v². (Donde obviamente .) Si s = 0 o s > 1, se eliminan u y v y se prueba con otro par (u, v). Se continúa con el proceso hasta que se encuentra un par con s en el intervalo abierto (0, 1). Dado que u y v están uniformemente distribuidos y como sólo se admiten puntos contenidos en el círculo unitario, los valores de s también se encontraran uniformemente distribuidos en el intervalo abierto (0, 1). Esto último se puede verificar si se calcula la función de densidad de probabilidad para s en el intervalo (0, 1). Lo que no es otra cosa que el área del círculo de radio dividido por . A partir de esto se puede encontrar la función de densidad de probabilidad que tenga un valor constante de 1 en el intervalo (0, 1). En forma similar, el ángulo θ dividido por está distribuido uniformemente en el intervalo abierto (0, 1) e independiente de s.

Referencias

1. ↑ G. E. P. Box and Mervin E. Müller, A Note on the Generation of Random Normal Deviates, The Annals of Mathematical Statistics (1958), Vol. 29, No. 2 pp. 610-611
2. ↑ Kloeden and Platen, Numerical Solutions of Stochastic Differential Equations, p. 11-12
3. ↑ Sheldon Ross, A First Course in Probability, (2002), p.279-81
4. ↑ L. Devroye: 'Non-Uniform Random Variate Generation', Springer-Verlag, New York, 1986.
5. ↑ Everett F. Carter, Jr., The Generation and Application of Random Numbers, Forth Dimensions (1994), Vol. 16, No. 1 & 2.

Enlaces externos

• Box-Müller que se ejecuta sobre un Applet Java
• Generación de números aleatorios gaussianos
• La transformada de Box-Müller -MathWorld