- NP (Complejidad computacional)
-
NP (Complejidad computacional)
Los recursos comúnmente estudiados en complejidad computacional son:
– El tiempo: mediante una aproximación al número de pasos de ejecución que un algoritmo emplea para resolver un problema.
– El espacio: mediante una aproximación a la cantidad de memoria utilizada para resolver el problema.
En el análisis computacional, se requiere un modelo de la computadora para la que desea estudiar el requerimiento en términos de tiempo. Normalmente, dichos modelos suponen que la computadora es determinista (dado el estado actual de la computadora y las variables de entrada, existe una única acción posible que la computadora puede tomar) y secuencial (realiza las acciones una después de la otra). Estas suposiciones son adecuadas para representar el comportamiento de todas las computadoras existentes, aún incluye a las máquinas con computación en paralelo.
Los problemas se clasifican en conjuntos o clases de complejidad (L, NL, P, P-Completo,NP, NP-Completo, NP Duro...).Nosotros nos vamos a centrar en la clase NP.
Contenido
La clase NP
En teoría de la complejidad computacional, NP es el acrónimo en inglés de Polinómico no determinista (Non-Deterministic Polynomial-time). Es el conjunto de problemas que pueden ser resueltos en tiempo polinómico por una máquina de Turing no determinista.
La importancia de esta clase de problemas de decisión es que contiene muchos problemas de búsqueda y de optimización para los que se desea saber si existe una cierta solución o si existe una mejor solución que las conocidas. En esta clase están el problema del viajante (también llamado "problema del agente de ventas" o "problema del agente viajero") donde se quiere saber si existe una ruta óptima que pasa por todos los nodos en un cierto grafo y el problema de satisfacibilidad booleana en donde se desea saber si una cierta fórmula de lógica proposicional puede ser cierta para algún conjunto de valores booleanos para las variables.
Dada su importancia, se han hecho muchos esfuerzos para encontrar algoritmos que decidan algún problema de NP en tiempo polinómico. Sin embargo, pareciera que para algunos problemas de NP (los del conjunto NP-completo) no es posible encontrar un algoritmo mejor que simplemente realizar una búsqueda exhaustiva.
En el artículo de 2002, "PRIMES is in P", Manindra Agrawal con sus estudiantes[1] ,[2] encontró un algoritmo que trabaja en tiempo polinómico para el problema de saber si un número es primo. Anteriormente se sabía que ese problema estaba en NP, si bien no en NP-completo, ahora se sabe que también está en P.
El primer problema natural que se demostró que es completo NP fue el problema de satisfacibilidad booleana. Este resultado fue demostrado por Stephen Cook en 1971, y se lo llamó el teorema de Cook. La demostración de Cook de que la satisfacibilidad es un problema NP-completo es muy complicada. Sin embargo, después de que este problema se demostrara que es NP-Completo, es fácil demostrar que muchos otros problemas pertenecen a esta clase. Por lo tanto, una amplia clase de problemas en principio inconexos son reducibles unos a otros, y por lo tanto resultan en "el mismo problema" -- un resultado profundo e inesperado.
Relación con otras clases de complejidad
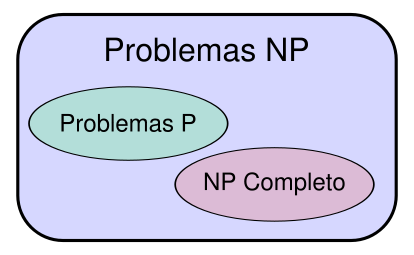
NP contiene todos los problemas pertenecientes a las clases P y NP-C, y a su vez está contenido en el conjunto de los PSPACE. Aún se desconoce si estas inclusiones son estrictas o no, y si la intersección entre los NP y Co-NP es o no vacía.
En particular, el mayor problema en ciencias de la computación consiste en responder al siguiente problema de decisión: ¿P=NP?
Ejemplo: Problema CLIQUE(Clique)
Denominamos CLIQUE al siguiente problema:
Dado un grafo G y un entero k, ¿es posible encontrar un subgrafo de G completo de tamaño k?
• Claramente CLIQUE pertenece a NP.
• Ahora deberemos hacer una reducción de SAT a NP.
• Supongamos que tenemos una fórmula en FNC:
C1 v C2 v . . . v Ck con n variables proposicionales.
Formaremos un grafo G con un nodo por cada literal que aparece en cada cláusula. Cada nodo está etiquetado con el literal que le dio origen.Agregaremos un arco entre un nodo etiquetado con l y un nodo etiquetado con l0 si y solo si:
– l y l0 están en cláusulas distintas.
– l no es el literal complementario de l.
Supongamos la siguiente fórmula: (x1 v x2 v ¬x3) ^ (¬x1 v ¬x3) ^ (x3 v x2). El grafo resultante queda como:
Archivo:Grafonuestro.jpg
Ahora deberemos demostrar que G tiene un subgrafo completo de tamaño k ssi es satisfactible. Como todos los miembros del subgrafo pertenecen a cláusulas distintas, cualquier valuación que hace verdadero a todo literal en el subgrafo hace verdadera a la fórmula(recordemos que dos literales complementarios no pueden estar en un subgrafo completo). Si la fórmula es satisfecha, debe existir una valuación que haga verdaderos a al menos un literal en cada cláusula. Sean l1 pertenece a C1, l2 pertenece a C2, . . . , lk pertenece Ck estos literales. Notemos que no es posible que existan dos literales complementarios li y lj. Necesariamente, entonces, podemos construir arcos entre cada par de nodos en donde aparecen dichos literales siguiendo las reglas de construcción del grafo.
Otros Ejemplos
Camino Máximo: Dados dos vértices de un grafo encontrar el camino (simple) máximo.
Ciclo Hamiltoniano: Ciclo simple que contiene cada vértice del grafo.
Referencias
- ↑ Agrawal, Manindra; Kayal, Neeraj; Saxena, Nitin: "PRIMES is in P". Annals of Mathematics 160 (2004), no. 2, pp. 781–793.
Accesible en formato PDF desde la web www.math.princeton.edu
- ↑ Sobre el artículo de Manindra Agrawal et al. "PRIMES is in P"
Categoría: Clases de complejidad - ↑ Agrawal, Manindra; Kayal, Neeraj; Saxena, Nitin: "PRIMES is in P". Annals of Mathematics 160 (2004), no. 2, pp. 781–793.
Wikimedia foundation. 2010.