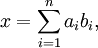Anillo de los números enteros

Anillo de los números enteros

Anillo de los números enteros


En matemáticas, la frase anillo de los números enteros se puede referir a

  • el anillo de todos los enteros (positivos, negativos o cero), usualmente indicado como Z.
  • dado un campo numérico algebraico K, los enteros algebraicos contenidos en K forman un anillo, el anillo de los enteros de K, comúnmente indicado como OK.

Usando esta notación, se puede escribir Z = OQ dado que Z es el anillo de enteros del campo Q de números racionales. Y en efecto por esta razón, en la teoría de números algebraicos los elementos de Z son comúnmente llamados los "enteros racionales".

El anillo de los números enteros OK tiene una base integral; lo que significa que existe b1,...,bn ∈ OK (la base integral) tal que cada elemento x en OK puede ser unívocamente representado como

x=\sum_{i=1}^na_ib_i,

con ai ∈ Z.

Si ζ es la p-iésima raíz de la unidad y K=Q(ζ) es el campo ciclotómico correspondiente, entonces una base integral de OK está dada por (1,ζ,ζ2,...,ζp-2).

Si d es un entero cuadrático libre y K=Q(d1/2) es el campo cuadrático correspondiente, entonces una base integral de OK está dada por (1,(1+d1/2)/2) si d≡1 (mod 4) y por (1,d1/2) si d≡2 or 3 (mod 4).

Obtenido de "Anillo de los n%C3%BAmeros enteros"

Wikimedia foundation. 2010.

Игры ⚽ Нужно сделать НИР?

Mira otros diccionarios:

  • Números primos entre sí — En matemáticas, dos números enteros a y b son números primos entre sí (o coprimos, o primos relativos), si, por definición, no tienen ningún factor primo en común, o, dicho de otra manera, si no tienen otro divisor común más que 1 y 1.… …   Wikipedia Español

  • Anillo conmutativo — Saltar a navegación, búsqueda En teoría de anillos (una rama del álgebra abstracta), un anillo conmutativo es un anillo (R, +, ·) en el que la operación de multiplicación · es conmutativa; es decir, si para cualesquiera a, b ∈ R, a·b = b·a. Si… …   Wikipedia Español

  • Anillo noetheriano — Saltar a navegación, búsqueda En álgebra, un anillo R es noetheriano por la izquierda si sus ideales por la izquierda satisfacen la condición de cadena ascendente. Diremos que un anillo es noetheriano si es noetheriano por la izquierda y por la… …   Wikipedia Español

  • Anillo (matemática) — En álgebra, un anillo es una estructura algebraica formada por un conjunto (A), y dos operaciones: suma y producto; de modo que (A,+) es un grupo conmutativo con elemento neutro (que designamos 0), y el producto es asociativo y tiene la propiedad …   Wikipedia Español

  • Anillo cíclico — Saltar a navegación, búsqueda Contenido 1 Definición 2 Cálculo elemental 3 Aplicaciones directas a la aritmética 4 …   Wikipedia Español

  • Anillo planetario — Saltar a navegación, búsqueda Un anillo planetario es un anillo de polvo y otras partículas pequeñas que gira alrededor de un planeta. Los más espectaculares y conocidos desde la época telescópica son los anillos de Saturno. Durante mucho tiempo… …   Wikipedia Español

  • Anillo ordenado — Saltar a navegación, búsqueda Definiciones En álgebra abstracta, un anillo ordenado es un anillo conmutativo R con un orden total tal que si y , entonces si …   Wikipedia Español

  • Anillo de polinomios — Saltar a navegación, búsqueda Sea A un anillo y S cualquier conjunto. El conjunto A[S] de todos los objetos (1) , en donde …   Wikipedia Español

  • Teoría de números algebraicos — La teoría de números algebraicos o teoría algebraica de números es una rama de la teoría de los números en la cual el concepto de número se expande a los números algebraicos, los cuales son las raíces de los polinomios con coeficientes racionales …   Wikipedia Español

  • Partícula en un anillo — Saltar a navegación, búsqueda La partícula en un anillo es un ejemplo sencillo de sistema cuántico con propiedades interesantes. Este modelo reproduce las características hipotéticas de una partícula libre que se mueve solamente a lo largo de un… …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”