- Anillo ordenado
-
Anillo ordenado
Definiciones
En álgebra abstracta, un anillo ordenado es un anillo conmutativo R con un orden total
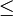tal que- si
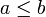y 
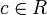, entonces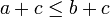 
- si
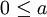y 
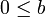, entonces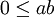 
Los anillos ordenados son propios de la aritmética. Algunos ejemplos incluyen los enteros, los racionales y los reales. (Los racionales y los reales son, de hecho, cuerpos ordenados). Por otra banda, los números complejos no forman un anillo ordenado (o cuerpo).
Análogamente con los números ordinarios, decimos que un elemento c de un anillo ordenado es positivo si
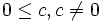y negativo si 
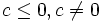. El conjunto de los elementos positivos en un anillo R suele ser denotado por R + .Si a es un elemento de un anillo ordenado R, entonces el valor absoluto de a, denotado por | a | , se define de la siguiente forma:
donde − a es el opuesto de a y 0 es el elemento neutro.
Propiedades básicas
- Si 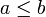y
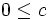, entonces 
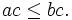Esta propiedad, a veces, se utiliza para definir anillos ordenados en lugar de la segunda propiedad en la definición de más arriba. - Si
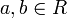, entonces | ab | = | a | | b | . - Un anillo ordenado no trivial es infinito.
- Si
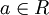, entonces 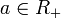o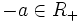 
, o 
, o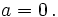 
Esta propiedad se deriva del hecho que los anillos ordenados son abelianos, con orden total respecto la suma. - Un anillo ordenado R no tiene divisores de cero si y solo si R + es cerrado respecto el producto, es decir, ab es positivo si ambos a y b son positivos.
Categoría: Teoría de anillos - si
Wikimedia foundation. 2010.
