Número poligonal

Número poligonal
Los números pentagonales son un caso especial de números poligonales, en donde la figura base tiene 5 lados.

En matemáticas, un número poligonal es un número que puede recomponerse en un polígono regular. Los matemáticos de la Antigüedad descubrieron que los números podían recomponerse de ciertas formas cuando los representaban con piedras o semillas.

Números poligonales

El número 10 puede recomponerse como un triángulo (ver número triangular):

*
**
***
****

Sin embargo, el 10 no puede formar un cuadrado, pero el 9 sí (véase número cuadrado):

***
***
***


Algunos números, como el 36, pueden recomponerse tanto en un cuadrado como en un triángulo (véase número cuadrado triangular):

******
******
******
******
******
******		 *
**
***
****
*****
******
*******
********


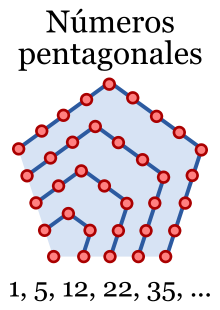
El método empleado para agrandar el polígono hasta el siguiente tamaño es extender dos brazos adyacentes por un punto y luego añadir los lados extra requeridos entre los puntos.

n-ésimo número poligonal

Si l es el número de lados de un polígono, entonces la fórmula para el n-ésimo número poligonal de l lados es \tfrac{n((l-2)n-(l-4))}{2}.


Nombre Fórmula n=1 2 3 4 5 6 7 8 9 10 11 12 13
Triangular ½n(1n + 1) 1 3 6 10 15 21 28 36 45 55 66 78 91
Cuadrado ½n(2n - 0) 1 4 9 16 25 36 49 64 81 100 121 144 169
Pentagonal ½n(3n - 1) 1 5 12 22 35 51 70 92 117 145 176 210 247
Hexagonal ½n(4n - 2) 1 6 15 28 45 66 91 120 153 190 231 276 325
Heptagonal ½n(5n - 3) 1 7 18 34 55 81 112 148 189 235 286 342 403
Octagonal ½n(6n - 4) 1 8 21 40 65 96 133 176 225 280 341 408 481
Nonagonal ½n(7n - 5) 1 9 24 46 75 111 154 204 261 325 396 474 559
Decagonal ½n(8n - 6) 1 10 27 52 85 126 175 232 297 370 451 540 637
11-agonal ½n(9n - 7) 1 11 30 58 95 141 196 260 333 415 506 606 715
12-agonal ½n(10n - 8) 1 12 33 64 105 156 217 288 369 460 561 672 793
13-agonal ½n(11n - 9) 1 13 36 70 115 171 238 316 405 505 616 738 871
14-agonal ½n(12n - 10) 1 14 39 76 125 186 259 344 441 550 671 804 949
15-agonal ½n(13n - 11) 1 15 42 82 135 201 280 372 477 595 726 870 1027
16-agonal ½n(14n - 12) 1 16 45 88 145 216 301 400 513 640 781 936 1105
17-agonal ½n(15n - 13) 1 17 48 94 155 231 322 428 549 685 836 1002 1183
18-agonal ½n(16n - 14) 1 18 51 100 165 246 343 456 585 730 891 1068 1261
19-agonal ½n(17n - 15) 1 19 54 106 175 261 364 484 621 775 946 1134 1339
20-agonal ½n(18n - 16) 1 20 57 112 185 276 385 512 657 820 1001 1200 1417
21-agonal ½n(19n - 17) 1 21 60 118 195 291 406 540 693 865 1056 1266 1495
22-agonal ½n(20n - 18) 1 22 63 124 205 306 427 568 729 910 1111 1332 1573
23-agonal ½n(21n - 19) 1 23 66 130 215 321 448 596 765 955 1166 1398 1651
24-agonal ½n(22n - 20) 1 24 69 136 225 336 469 624 801 1000 1221 1464 1729
25-agonal ½n(23n - 21) 1 25 72 142 235 351 491 652 837 1045 1276 1530 1807
26-agonal ½n(24n - 22) 1 26 75 148 245 366 511 680 873 1090 1331 1596 1885
27-agonal ½n(25n - 23) 1 27 78 154 255 381 532 708 909 1135 1386 1662 1963
28-agonal ½n(26n - 24) 1 28 81 160 265 396 553 736 945 1180 1441 1728 2041
29-agonal ½n(27n - 25) 1 29 84 166 275 411 574 764 981 1225 1496 1794 2119
30-agonal ½n(28n - 26) 1 30 87 172 285 426 595 792 1017 1270 1551 1860 2197

Referencia


Wikimedia foundation. 2010.

Игры ⚽ Поможем решить контрольную работу

Mira otros diccionarios:

  • Número poligonal — En matemáticas, un número poligonal es un número que puede recomponerse en un polígono regular. Los matemáticos de la Antigüedad descubrieron que los números podían recomponerse de ciertas formas cuando los representaban con piedras o semillas.… …   Enciclopedia Universal

  • Teorema del número poligonal de Fermat — El teorema del número poligonal de Fermat dice que cada número natural es suma de a lo máximo n números poligonales. Cada número natural puede ser escrito como la suma de tres o menos números triangulares, o cuatro o menos números cuadrados, o… …   Wikipedia Español

  • Número triangular — Se muestran los seis primeros números triangulares, así como su término general. Además de la denotación expuesta, un número triangular puede indicarse poniendo entre paréntesis el lado del triángulo correspondiente. Por ejemplo, el 10 es el… …   Wikipedia Español

  • Número hexagonal — Un número hexagonal es un número poligonal que se puede representar en forma de hexágono. La fórmula para un número hexagonal n es: Los primeros números hexagonales (sucesión A000384 en OEIS) son: 1, 6, 15, 2 …   Wikipedia Español

  • Pierre de Fermat — Saltar a navegación, búsqueda Pierre de Fermat Jurista y destacado matemático …   Wikipedia Español

  • Teorema de los cuatro cuadrados — El teorema de los cuatro cuadrados de Lagrange, también conocido como la conjetura de Bachet se demostró en 1770 por Joseph Louis Lagrange. Dice que cada número entero positivo puede expresarse como la suma de cuatro cuadrados de enteros. Por… …   Wikipedia Español

  • Teorema de los cuatro cuadrados — El teorema de los cuatro cuadrados de Lagrange , también conocido como la conjetura de Bachet se demostró en 1770 por Joseph Louis Lagrange. Dice que cada número entero puede expresarse como la suma de cuatro cuadrados de enteros. Por ejemplo, 31 …   Enciclopedia Universal

  • Augustin Louis Cauchy — Augustin Louis Cauchy. Nacimiento 21 de agosto de 1789 [[Archivo:{{{bandera alias 1638}}}|20x20px|border|link=|Bandera d …   Wikipedia Español

  • Teorema de Fermat — Existen varios teoremas en diversas áreas de la matemática que son denominados teorema de Fermat: En análisis matemático, el teorema de Fermat (análisis) un resultado sobre máximos y mínimos locales. En óptica el principio de Fermat. En teoría de …   Wikipedia Español

  • Tláhuac — Delegación Tláhuac Delegación de México …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”