- Politopo de cruce
-
En geometría, un politopo de cruce u ortoplex, es un politopo regular convexo que existe en cualquier número de dimensiones. Los vértices de un politopo de cruce consisten de todas las permutaciones de (±1, 0, 0, …, 0). El politopo de cruce es el casco o envoltorio convexo de sus vértices. (Nota: algunos autores definen al politopo convexo sólo como la envoltura de esta región).
En una dimensión, el politopo de cruce es simplemente un segmento de línea [−1, +1], en dos dimensiones es el cuadrado con vértices {(±1, 0), (0, ±1)}. En tres dimensiones es el octaedro (uno de los cinco poliedros conocidos como sólidos platónicos. Los politopos de cruce en mayor número de dimensiones son generalizaciones de estos.
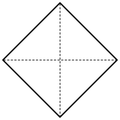
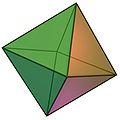
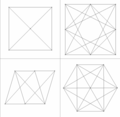
2 dimensiones 3 dimensiones 4 dimensiones El politopo de cruce es el dual del politopo de medida.
Cuatro dimensiones
El politopo de cruce de cuatro dimensiones tiene el nombre de hexadecacoron o 16-cell, uno de los seis polícoros regulares. Estos polícoros fueron descriptos originalmente por el matemático suizo Ludwig Schläfli a mediados del siglo XIX.
Dimensiones mayores
En n dimensiones con n > 4 existen sólo tres politopos regulares: el simplex, el politopo de medida, y el politopo de cruce, siendo estos dos últimos duales y el simplex auto-dual.
El politopo de cruce n-dimensional tiene 2n vértices, y 2n facetas (componentes (n−1)-dimensionales) todos los cuales son n−1-simplices. Las figuras de vértice son todas politopos de cruce (n−1)dimensionales. El símbolo de Schläfli del politopo de cruce es {3,3,…,3,4}.
El número de componentes k-dimensionales (vértices, aristas, caras, …, facetas) de un politopo de cruce n-dimensional está determinado por (ver coeficiente binomial):
Para los primeros n y k tendremos:
n\k 0 1 2 3 4 1 2 2 4 4 3 6 12 8 4 8 24 32 16 5 10 40 80 80 32 Véase también
- Lista de politopos regulares
Wikimedia foundation. 2010.

