Politopos regulares convexos de 4 dimensiones
- Politopos regulares convexos de 4 dimensiones
-
Politopos regulares convexos de 4 dimensiones
En matemáticas, un politopo regular convexo de 4 dimensiones (o polícoro) es un politopo tetradimensional que al mismo tiempo es regular y convexo. Son los análogos en cuatro dimensiones de los sólidos platónicos en tres dimensiones y los polígonos regulares en dos dimensiones.
Ludwig Schläfli
Estos politopos fueron descriptos por primera vez por el matemático suizo Ludwig Schläfli a mediados del siglo XIX. Schläfli descubrió que hay precisamente 6 de estas figuras. Cinco de ellas pueden pensarse como análogos de los sólidos platónicos en mayor número de dimensiones. Hay una figura adicional, el icositetracoron o 24-cell, que no tiene un equivalente tridimensional.
Cada politopo regular convexo tetradimensional está delimitado por un conjunto de celdas tridimensionales, que son todas sólidos platónicos del mismo tipo y tamaño. Se agrupan a lo largo de sus respectivas caras de modo regular.
Politopos regulares de 4 dimensiones
| Nombre |
Familia |
Símbolo de
Schläfli |
Vértices |
Aristas |
Caras |
Celdas |
Figuras de
vértices |
Politopo dual |
Imagen |
| pentácoron |
simplex |
{3,3,3} |
5 |
10 |
10
triángulos |
5
tetraedros |
tetraedros |
(auto-dual) |
 |
| teseracto |
politopo de medida |
{4,3,3} |
16 |
32 |
24
cuadrados |
8
cubos |
tetraedros |
16-cell |
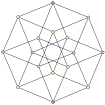 |
hexadecacoron
o 16-cell |
politopo de cruce |
{3,3,4} |
8 |
24 |
32
triángulos |
16
tetraedros |
octaedros |
teseracto |
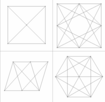 |
icositetracoron
o 24-cell |
|
{3,4,3} |
24 |
96 |
96
triángulos |
24
octaedros |
cubos |
(auto-dual) |
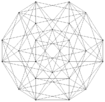 |
hecatonicosacoron
o 120-cell |
|
{5,3,3} |
600 |
1200 |
720
pentágonos |
120
dodecaedros |
tetraedros |
600-cell |
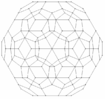 |
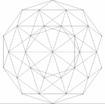
hexacosicoron
o 600-cell |
|
{3,3,5} |
120 |
720 |
1200
triángulos |
600
tetraedros |
icosaedros |
120-cell |
 |
Nótese que puesto que cada una de estas figuras es topológicamente equivalente a una 3-esfera, cuya característica de Euler es cero, tenemos el análogo tetradimensional de la fórmula poliédrica de Euler
- N0 − N1 + N2 − N3 = 0
donde Nk denota el número de k-caras del politopo (un vértice es una 0-cara, una arista es una 1-cara, etc.).
Véase también
- Politopos semiregulares de 4 dimensiones
- Politopo regular
- Lista de politopos regulares
- Sólido platónico
Referencias
- H. S. M. Coxeter, Introduction to Geometry, 2nd ed., John Wiley & Sons Inc., 1969. ISBN 0-471-50458-0.
Enlaces externos
La versión original de este artículo es una traducción de en:Convex regular 4-polytope en Wikipedia en inglés
Categorías: Politopos | Geometría tetradimensional
Wikimedia foundation.
2010.
Mira otros diccionarios:
Politopos regulares convexos de 4 dimensiones — En matemáticas, un politopo regular convexo de 4 dimensiones (o polícoro) es un politopo tetradimensional que al mismo tiempo es regular y convexo. Son los análogos en cuatro dimensiones de los sólidos platónicos en tres dimensiones y los… … Enciclopedia Universal
Politopo regular — Saltar a navegación, búsqueda Un dodecaedro, uno de los cinco sólidos platónicos. En Matemáticas, un politopo regular es una figura geométrica con un alto grado de simetría. Ejemplo de politopos regulares en dos dim … Wikipedia Español
Pentácoron — Proyección ortográfica de un polícoron en dos dimensiones. El pentácoron, también llamado pentácoro, pentatopo o 4 simplex es el más simple de los politopos regulares convexos de 4 dimensiones, un tipo de figura geométrica tetradimensional. Es un … Wikipedia Español
Hecatonicosacoron — En geometría un hecatonicosacoron o 120 cell es uno de los seis politopos regulares convexos de 4 dimensiones, con símbolo de Schläfli {5,3,3}. Se lo considera a veces como el análogo tetradimensional del dodecaedro, razón por la que suele ser… … Wikipedia Español
Hexadecacoron — El hexadecacoron o 16 cell es uno de los seis politopos regulares convexos de 4 dimensiones. Estos polícoros fueron descritos por vez primera por el matemático suizo Ludwig Schläfli a mediados del siglo XIX. Proyecciones del Hexadecacoron. El… … Wikipedia Español
Hexacosicoron — En geometría, el hexacosicoron o 600 cell, es uno de los politopos regulares convexos de 4 dimensiones, con símbolo de Schläfli {3, 3, 5}. Se lo considera a veces el análogo en cuatro dimensiones del icosaedro, razón por la cual se lo llama… … Wikipedia Español
Polícoro — Saltar a navegación, búsqueda El hipercubo es el polícoro mejor conocido: posee ocho celdas cúbicas, tres alrededor de cada borde. Está representado como diagrama de Schlegel, en una proyección de un espacio tridimensional, distorsionando su… … Wikipedia Español
Hexadecacoron — El hexadecacoron o 16 cell es uno de los seis politopos regulares convexos de 4 dimensiones. Estos polícoros fueron descriptos por vez primera por el matemático suizo Ludwig Schläfli a mediados del siglo XIX. El hexadecacoron tiene 16 celdas,… … Enciclopedia Universal
Hexacosicoron — En geometría, el hexacosicoron o 600 cell , es uno de los politopos regulares convexos de 4 dimensiones, con símbolo de Schläfli 3,3,5. Se lo considera a veces el análogo en cuatro dimensiones del icosaedro, razón por la cual se lo llama también… … Enciclopedia Universal
Pentácoron — El pentácoron, también llamado pentácoro, pentatopo o 4 simplex es el más simple de los politopos regulares convexos de 4 dimensiones, un tipo de figura geométrica de tetradimensional. Es un análogo del triángulo en el plano y el tetraedro entre… … Enciclopedia Universal






