- Convergencia
-
Convergencia
En análisis matemático, el concepto de convergencia hace referencia a la propiedad que poseen algunas sucesiones numéricas de tender a un límite. Este concepto es bien general y dependiendo de la naturaleza del conjunto donde se encuentre definida la sucesión, puede adoptar varias formas.
Contenido
Definición
Una sucesión de elementos
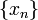 de un espacio métrico
de un espacio métrico 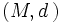 converge a un elemento
converge a un elemento 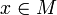 si para todo número
si para todo número 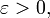 existe un entero positivo
existe un entero positivo 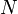 (que depende de
(que depende de  ) tal que
) tal que(1)

En tal caso, se acostumbra escribir
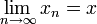
o también
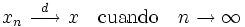
o simplemente
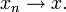
Intuitivamente, esto significa que los elementos
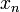 de la sucesión se pueden hacer arbitrariamente cercanos a
de la sucesión se pueden hacer arbitrariamente cercanos a 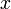 si
si 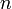 es suficientemente grande, ya que
es suficientemente grande, ya que 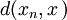 determina la distancia entre
determina la distancia entre 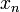 y
y 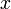 . A partir de la definición es posible demostrar que si una sucesión converge, lo hace hacia un único límite.
. A partir de la definición es posible demostrar que si una sucesión converge, lo hace hacia un único límite.La definición se aplica en particular a los espacios vectoriales normados y a los espacios con producto interno. En el caso de un espacio normado
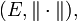 la norma
la norma  induce la métrica
induce la métrica 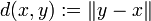 para cada
para cada 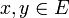 ; en el caso de un espacio con producto interno
; en el caso de un espacio con producto interno 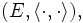 el producto interno
el producto interno 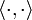 induce la norma
induce la norma 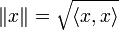 para cada
para cada 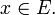
Ejemplos
- Sucesiones en
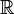 ó
ó 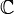
El conjunto de los números reales
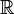 al igual que el conjunto de los números complejos
al igual que el conjunto de los números complejos 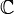 se constituyen en un espacio métrico por medio del valor absoluto: para cada par de elementos
se constituyen en un espacio métrico por medio del valor absoluto: para cada par de elementos 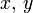 en
en 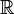 ó
ó 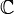 , la función
, la función 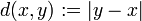 determina una métrica.
determina una métrica.Por tanto, de acuerdo a (), una sucesión
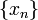 en
en 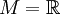 converge a un
converge a un 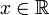 si para todo
si para todo 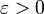 , existe un entero
, existe un entero 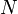 tal que
tal que
Como ejemplos podemos considerar:
-
- La sucesión constante definida por
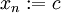 para todo
para todo 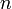 , donde
, donde 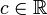 . Esta sucesión converge a
. Esta sucesión converge a  pues
pues
- La sucesión constante definida por
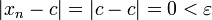
-
- para todo
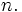
- para todo
-
- La sucesión
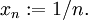 Esta sucesión converge a cero, pues por la propiedad arquimediana de los números reales, para cada
Esta sucesión converge a cero, pues por la propiedad arquimediana de los números reales, para cada 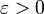 , exite número natural
, exite número natural 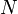 tal que
tal que 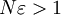 y por tanto, si
y por tanto, si 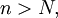
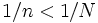 y
y
- La sucesión
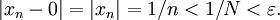
-
- La sucesión del ejemplo anterior es un caso particular de un resultado más general. Dado
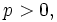
- La sucesión del ejemplo anterior es un caso particular de un resultado más general. Dado
![\lim_{n\to \infty}\frac{1}{n^p}=0\, , \quad \lim_{n\to \infty}\sqrt[n]{p}=1\,, \quad \lim_{n\to \infty}\sqrt[n]{n}=1](/pictures/eswiki/55/7c250fe708538069deee30e78b593097.png)
-
- Si
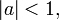 entonces
entonces 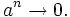
- Si
-
- La sucesión
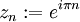 . Esta sucesión no converge, sus valores oscilantes son
. Esta sucesión no converge, sus valores oscilantes son 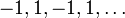
- La sucesión
-
- Debido a que
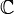 (en particular
(en particular 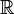 ) está dotado de una operación suma (lo que no ocurre en todo espacio métrico), a cada sucesión
) está dotado de una operación suma (lo que no ocurre en todo espacio métrico), a cada sucesión 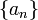 en
en 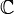 (en particular
(en particular 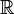 ) es posible asociarle la sucesión de sumas parciales
) es posible asociarle la sucesión de sumas parciales
- Debido a que
(2)
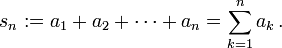
-
- La sucesión
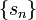 se expresa simbólicamente como
se expresa simbólicamente como
- La sucesión
(3)
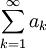
-
- y se le denomina serie infinita. En el caso en que la sucesión de sumas parciales () converja,
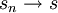 , se dice que () es una serie convergente y se escribe
, se dice que () es una serie convergente y se escribe
- y se le denomina serie infinita. En el caso en que la sucesión de sumas parciales () converja,
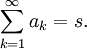
-
- En caso contrario se dice que () es una serie divergente. Ejemplos clásicos de series convergentes y divergentes son
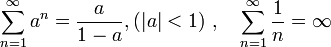
Observemos que la definición de convergencia nos dice que una sucesión
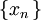 en un espacio métrico
en un espacio métrico 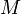 converge a un
converge a un 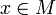 si la sucesión de números reales
si la sucesión de números reales 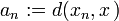 converge a cero en
converge a cero en 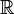 , i.e.,
, i.e.,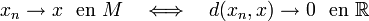
- Sucesiones en
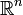
- Sucesiones en el espacio
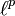
- Sucesiones en el espacio
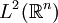
- Sucesiones en el espacio de las funciones continuas
![C[a,b]\,](/pictures/eswiki/49/12dc259d5b0ea6bb39558142e2a0f27d.png)
Sucesiones de Cauchy
Para determinar la convergencia de una sucesión a partir de la definición es necesario conocer de antemano el elemento hacia el cual ésta converge. Dicha información por lo general se desconoce. Para una gran variedad de espacios, existe un criterio para determinar la convergencia de una sucesión sin conocer su límite.
Una sucesión
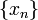 en un espacio métrico
en un espacio métrico 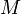 es una sucesión de Cauchy si para todo
es una sucesión de Cauchy si para todo 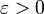 , existe un entero positivo
, existe un entero positivo 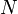 (que depende de
(que depende de  ) tal que
) tal que(4)
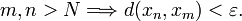
Intuitivamente, esto signfica que la distancia entre los elementos
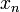 y
y 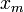 de la sucesión se hace arbritrariamente pequeña si
de la sucesión se hace arbritrariamente pequeña si 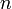 y
y 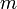 son lo suficientemente grandes.
son lo suficientemente grandes.Si
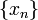 es una sucesión convergente, existe un
es una sucesión convergente, existe un 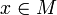 tal que
tal que 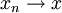 y por la desigualdad triangular,
y por la desigualdad triangular,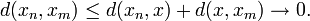
Por lo tanto, toda sucesión convergente es de Cauchy. Sin embargo, el enunciado recíproco no siempre es válido y no toda sucesión de Cauchy es convergente: la sucesión de números racionales
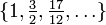 definida por
definida por 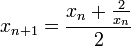 para
para 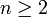 con
con 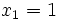 es una sucesión de Cauchy en
es una sucesión de Cauchy en 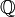 que no es convergente, pues su límite es el número irracional
que no es convergente, pues su límite es el número irracional 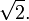
Un espacio métrico en el que toda sucesión de Cauchy es convergente se denomina completo. Los racionales son un ejemplo de un espacio que no es completo mientras que
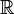 y
y 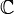 constituyen ejemplos de espacios métricos completos. Por consiguiente, una condición suficiente y necesaria para que una sucesión
constituyen ejemplos de espacios métricos completos. Por consiguiente, una condición suficiente y necesaria para que una sucesión 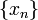 de números reales (o complejos) converja, viene dada por (), con
de números reales (o complejos) converja, viene dada por (), con 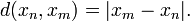 En particular, cuando la condición se aplica a la sucesión de sumas parciales (),
En particular, cuando la condición se aplica a la sucesión de sumas parciales (),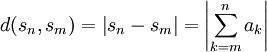
y se obtiene el criterio de convergencia de Cauchy: una serie
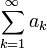 es convergente si, y sólo si, para todo
es convergente si, y sólo si, para todo 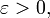 existe un entero
existe un entero 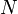 tal que
tal que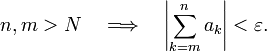
A los espacios vectoriales normados y completos se les denominan espacios de Banach en honor al trabajo desarrollado por el matemático polaco Stefan Banach. Estos espacios constituyen uno de los objetos centrales de estudio del análisis funcional. Ejemplos de espacios de Banach comunes son
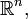
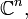 el espacio
el espacio 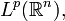 el espacio
el espacio 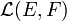 de los operadores lineales continuos de un espacio vectorial
de los operadores lineales continuos de un espacio vectorial 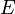 en un espacio vectorial
en un espacio vectorial 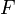 y el espacio de la funciones continuas con valores complejos
y el espacio de la funciones continuas con valores complejos 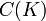 con
con 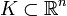 compacto.
compacto.Los espacios de Banach cuya norma proviene de un producto interno se denominan espacios de Hilbert, en reconocimiento al trabajo desarrollado por el matemático alemán David Hilbert a comienzos del siglo XX. Ejemplos de espacios de Hilbert son
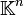 con
con 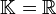 ó
ó 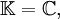 el espacio de las sucesiones complejas cuadrado-sumables
el espacio de las sucesiones complejas cuadrado-sumables 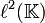 y el espacio de las funciones cuadrado-integrables en el sentido de Lebesgue
y el espacio de las funciones cuadrado-integrables en el sentido de Lebesgue 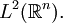 Una gran variedad de espacios de Hilbert que se presentan en la práctica son separables y son en particular los espacios
Una gran variedad de espacios de Hilbert que se presentan en la práctica son separables y son en particular los espacios 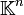 y
y 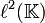 los prototipos principales de espacios de Hilbert, pues todo espacio de Hilbert separable de dimensión finita
los prototipos principales de espacios de Hilbert, pues todo espacio de Hilbert separable de dimensión finita 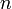 es isomorfo a
es isomorfo a 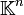 mientras que todo espacio de Hilbert separable de dimensión infinita es isomorfo a
mientras que todo espacio de Hilbert separable de dimensión infinita es isomorfo a 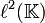 .
.Tipos de convergencia
Los varios tipos de convergencia se obtiene principalmente por hacer modificaciones menores en la definición básica. He aquí los tipos de convergencia más comunes: (Las diferencias entre sus definiciones y la definición básica se marca en cursiva.)
Convergencia puntual
El concepto de convergencia puntual es uno de los varios sentidos en los cuales una sucesión de funciones puede converger a una función particular.
Una sucesión de funciones
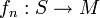 definidas en un conjunto no vacío
definidas en un conjunto no vacío 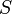 con valores en un espacio métrico
con valores en un espacio métrico 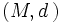 converge puntualmente a una función
converge puntualmente a una función 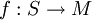 si
si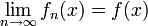
para cada
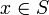 fijo. Esto significa que
fijo. Esto significa que(5)
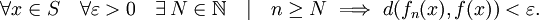
La sucesión de funciones
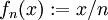 con
con ![x\in [0,1]](/pictures/eswiki/99/c628ba2b1047de93f66cb815d986e107.png) converge puntualmente a la función
converge puntualmente a la función 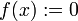 puesto que
puesto que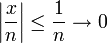
para cada
![x\in [0,1]](/pictures/eswiki/99/c628ba2b1047de93f66cb815d986e107.png) fijo.
fijo.Convergencia uniforme
Una sucesión de funciones
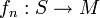 definidas en un conjunto no vacío
definidas en un conjunto no vacío 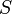 con valores en un espacio métrico
con valores en un espacio métrico 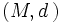 converge uniformemente a una función
converge uniformemente a una función 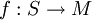 si para todo
si para todo 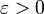 existe un entero
existe un entero 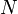 (que depende de
(que depende de  ) tal que
) tal que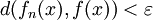
para todo
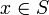 y todo
y todo 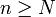 . Es decir,
. Es decir,(6)
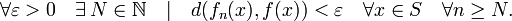
El concepto de convergencia uniforme es un concepto más fuerte que el de convergencia puntual. En (),
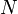 puede depender de
puede depender de  y de
y de 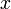 mientras que en (),
mientras que en (), 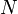 sólo puede depender de
sólo puede depender de  . Así, toda sucesión que converge uniformemente, converge puntualmente. El enunciado recíproco es falso, y un contraejemplo clásico lo constituyen las sucesión de funciones
. Así, toda sucesión que converge uniformemente, converge puntualmente. El enunciado recíproco es falso, y un contraejemplo clásico lo constituyen las sucesión de funciones ![f_n:[0,1]\to \mathbb R](/pictures/eswiki/57/9e277977259edf367a0c03421540ce45.png) definidas por
definidas por 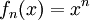 . Esta sucesión converge puntualmente a la función
. Esta sucesión converge puntualmente a la función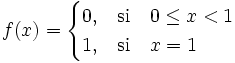
ya que
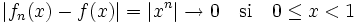
mientras que
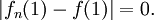 Sin embargo esta sucesión no converge uniformemente, pues para
Sin embargo esta sucesión no converge uniformemente, pues para 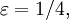 no existe un
no existe un 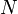 que satisfaga ().
que satisfaga ().De especial interés es el espacio de las funciones continuas
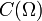 definidas sobre un compacto
definidas sobre un compacto 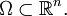 En este caso, una sucesión de funciones
En este caso, una sucesión de funciones 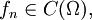 converge uniformemente a una función
converge uniformemente a una función 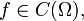 si, y sólo si, converge en la norma del sup, i.e.,
si, y sólo si, converge en la norma del sup, i.e.,
Convergencia uniforme sobre compactos
Convergencia débil
Una sucesion se dice que converge debilmente a x o en sentido debil si para toda funcional lineal f, f(Xn) converge a x.
Por ejemplo la serie 1/n desde n=1 hasta infinito converge débilmente a cero. Pues: lim f(1/n) = lim n/n*f(1/n) = lim 1/n*f(n/n) = lim 1/n*f(1) = 0 Todo esto, pues f es lineal.
Convergencia en espacios topológicos
Categorías: Wikipedia:Fusionar | Sucesiones | Series matemáticas - Sucesiones en
Wikimedia foundation. 2010.
