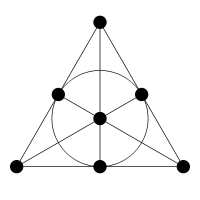
El plano de Fano es un ejemplo de Plano proyectivo

El plano proyectivo es el conjunto estudiado por la Geometría proyectiva. Surge en Geometría analítica al añadir a un plano un punto por cada familia de rectas paralelas (es decir, uno por cada par de direcciones opuestas). Los puntos así añadidos reciben el nombre de puntos del infinito, y su introducción unifica y simplifica mucho los enunciados de la geometría. Por ejemplo, la afirmación que dice que dos rectas de un plano se cortan en un único punto o son paralelas, en el plano proyectivo se enuncia: Dos rectas siempre se cortan en un único punto.

Empleo en la Geometría Proyectiva

La Geometría proyectiva surge realmente al estudiar "solamente" las relaciones de incidencia cuando los puntos ordinarios y los puntos del infinito se consideran en pie de igualdad. Una forma de visualizar la geometría proyectiva es tomar un punto P exterior al plano y definirla como las proyecciones de los elementos tridimensionales sobre un plano. Cada punto del plano define claramente una recta que pasa por P; pero así no obtenemos todas las rectas que pasan por P: faltan las rectas paralelas al plano dado, que se corresponden precisamente con las direcciones del plano.

Los puntos del plano proyectivo se corresponden naturalmente con las rectas que pasan por P, y las rectas del plano proyectivo con los planos que pasan por P. Esta correspondencia conserva las relaciones de incidencia, es un Isomorfismo entre sus respectivas estructuras. Podemos definir sin más el plano proyectivo como la radiación de rectas de vértice un punto dado P. Además esta perspectiva permite introducir también la recta proyectiva, como radiación de rectas de vértice dado en un plano, y espacios proyectivos tridimensionales, como radiación de rectas que pasan por el origen en un espacio vectorial de dimensión 4, o de cualquier otra dimensión n (sin más que considerar espacios vectoriales de dimensión n+1).

De la Pobreza de enunciados a su riqueza

Viendo sus dos principios (dos rectas se cortan en un punto y dos puntos definen una recta), la geometría proyectiva parece la más pobre de todas las geometrías, pues en sus enunciados sólo interviene el concepto de incidencia. No admite los conceptos de paralelismo, de perpendicularidad, distancia o ángulo. Solo permite enunciados de incidencia tales como:

• «Por dos puntos pasa una única recta» o bien
• Teorema de Desargues: «Si las tres rectas que unen los vértices de dos triángulos concurren en un punto, entonces los tres puntos de corte de las prolongaciones de los lados correspondientes están alineados».

Sin embargo, según hemos visto, los enunciados geométricos en que además interviene el concepto de paralelismo (la llamada Geometría afín) pueden reformularse en el plano proyectivo sin más que fijar una recta, recta que entonces recibe el nombre de «recta del infinito». Así, todo enunciado afín admite un enunciado proyectivo equivalente, y la Geometría afín puede verse como una pequeña parte de la Geometría proyectiva: Es la Geometría de un plano proyectivo con una recta prefijada (o un plano en el espacio proyectivo, etc.). Igualmente se vio que la geometría euclídea se obtiene al fijar dos puntos complejos conjugados en la recta del infinito (los puntos donde cortan todas las circunferencias), quedando así englobada en la Geometría proyectiva: Es la Geometría de un plano proyectivo donde se han fijado dos puntos complejos conjugados de una recta. Incluso la Geometría hiperbólica, la primera de las geometrías no euclídeas, puede obtenerse fijando una cónica: los puntos de la geometría son los puntos interiores de la cónica, las rectas son las secciones del interior de la cónica con rectas, y la distancia entre dos puntos A, B es esencialmente su razón doble con los puntos de corte P, Q de la recta AB con la cónica dada:

d(A,B) := | ln(A,B;P,Q) |

De este modo, la Geometría proyectiva, la más humilde de todas, pasó a ser «la reina de la Geometría».

Los Axiomas y Teoremas

Pero aún nos queda abordar la cuestión de la estructura subyacente en la Geometría proyectiva, de explicitar sus axiomas. Los geómetras alemanes del siglo XIX alcanzaron a exponerla considerando el retículo formado por las subvariedades lineales (puntos, rectas, planos, etc.). Lo caracterizaron como un retículo de dimensión 3 (en el caso del espacio) con las siguientes propiedades:

1. dim(A+B) = dim(A) + dim(B) - dim(A∩B)
2. Hay 5 puntos en posición general (ningún plano pasa por 4 de ellos).
3. Es válido el Teorema de Desargues.

La contribución española

Si se desea que el cuerpo de coordenadas sea conmutativo, se ha de imponer la validez del Teorema de Pappus. De hecho, el catedrático de instituto Ventura Reyes Prósper (Castuera, 31 de mayo de 1863 -- Toledo, 27 de noviembre de 1922) escribió una carta a Pasch explicando cómo en el espacio el Teorema de Desargues se sigue de las otra dos propiedades y es, por tanto, superfluo. Pasch, asombrado ante la sencillez del argumento («... auf denkbar einfachste Art...») que simplificaba notablemente su reciente libro, lo publicó en 1888 en los Matematische Annalen. Es la primera contribución española publicada en revista de tal importancia. En el caso del plano proyectivo, obviamente se ha de exigir que se un retículo de dimensión con 4 puntos en posición general (ninguna recta pasa por 3 de ellos); pero en tal caso el Teorema de Desargues ya no es consecuencia de las otras dos propiedades, sino que debe seguir manteniéndose como un axioma adicional.

En pleno siglo XX

Pero la sencilla recta proyectiva se resiste a ser caracterizada como retículo, pues su relación de orden es absolutamente trivial. Hasta mediados del siglo XX no se logró un marco conceptual que englobase tanto la estructura de la recta proyectiva como la del plano y el espacio proyectivo. El concepto de «esquema» introducido por Grothendieck permite recogerlos en su seno y, como regalo sobreabundante, también todo el Álgebra conmutativa y gran parte de la Aritmética.

Referencias

• D. Hughes and F. Piper,"Projective Planes", Springer-Verlag, 1973, ISBN 0-387-90044-6
• Clement W.H. Lam, "The Search for a Finite Projective Plane of Order 10", American Mathematical Monthly 98, (no. 4) 1991, pp.305 - 318.
• Lindner, Charles C. and Christopher A. Rodger (eds.) Design Theory, CRC-Press; 1 edition (October 31, 1997). ISBN 0-8493-3986-3.
• G. Eric Moorhouse, Projective Planes of Small Order, (2003)